MEDIDAS DE POSICIÓN (CUARTIL, DECIL, PERCENTIL) - DATOS AGRUPADOS
Summary
TLDREn este video se exploran las medidas de posición para datos agrupados en estadística, tales como cuartiles, deciles y percentiles. A lo largo de la lección, se detallan las fórmulas y métodos para calcular cada una de estas medidas, utilizando un conjunto de datos sobre las edades de pacientes en un consultorio médico. Se explica el paso a paso para encontrar la posición de cada medida, así como el procedimiento para resolver los cálculos, con ejemplos prácticos de cuartiles, deciles y percentiles. El video concluye con el análisis de los resultados y su interpretación estadística.
Takeaways
- 😀 Los percentiles son medidas de posición que dividen un conjunto de datos ordenado en 100 partes iguales.
- 😀 El cálculo de percentiles, como el P95, implica encontrar la posición en el conjunto de datos y aplicar una fórmula de interpolación.
- 😀 Para calcular percentiles, se utiliza la fórmula: Pk = L + ((n * k / 100) - F) * (h / f), donde L es el límite inferior del intervalo, n es el número total de datos, k es el percentil deseado, F es la frecuencia acumulada antes del intervalo, h es el ancho del intervalo, y f es la frecuencia del intervalo.
- 😀 El percentil 95 (P95) representa el valor debajo del cual se encuentra el 95% de los datos en el conjunto ordenado.
- 😀 El cálculo de percentiles requiere la identificación de la frecuencia acumulada y la posición dentro del intervalo correspondiente.
- 😀 Los datos agrupados en clases son esenciales para el cálculo preciso de percentiles, ya que se trabaja con frecuencias acumuladas.
- 😀 En el ejemplo, se muestra cómo calcular el P95 de un conjunto de datos de edades de pacientes, lo que da como resultado un valor aproximado de 77.33 años.
- 😀 Las medidas de posición, como los percentiles, se utilizan para analizar la distribución de datos y realizar interpretaciones estadísticas significativas.
- 😀 Es importante recordar que existen varios tipos de medidas de posición, como los cuartiles, deciles y percentiles, cada uno dividiendo los datos en diferentes cantidades de partes iguales.
- 😀 El proceso de cálculo de percentiles implica tanto la comprensión teórica como la aplicación práctica de fórmulas estadísticas, lo que facilita el análisis y la visualización de los datos.
- 😀 Con la correcta aplicación de fórmulas y la organización de los datos, se pueden interpretar con precisión las medidas de posición y su relevancia en estudios estadísticos y análisis de datos.
Q & A
¿Qué son las medidas de posición en estadística?
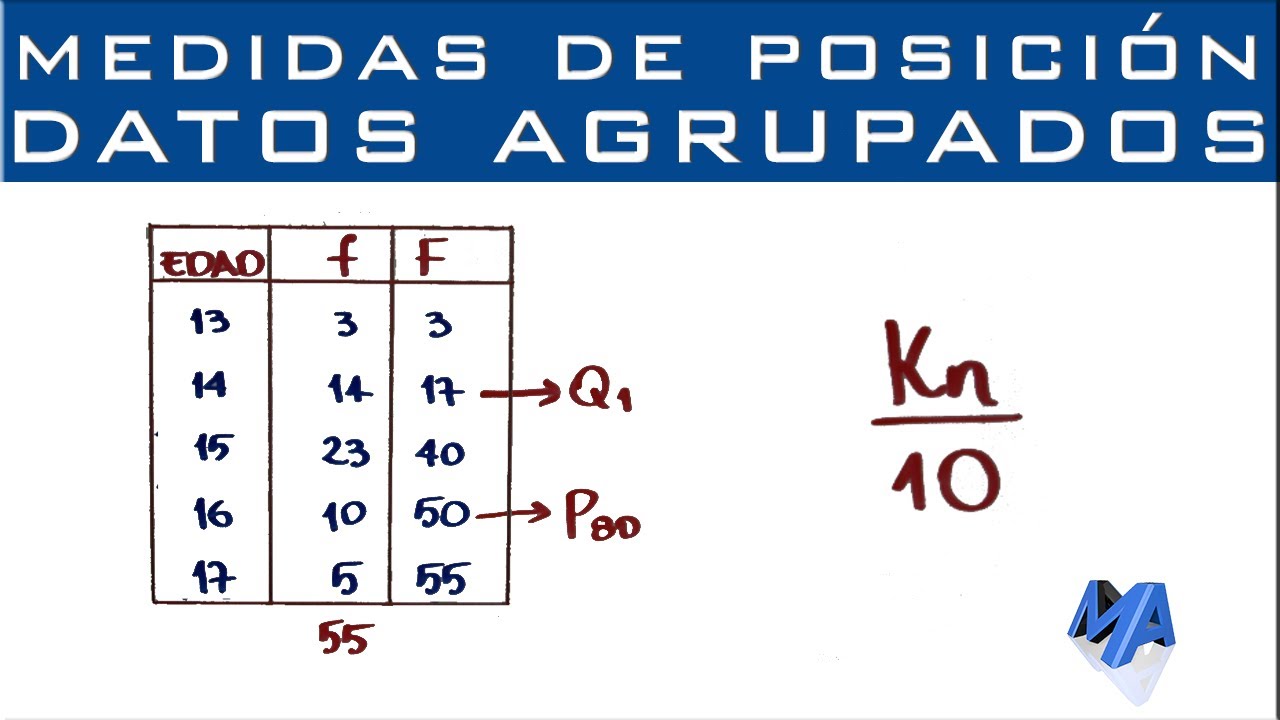
-Las medidas de posición son valores que permiten dividir un conjunto de datos ordenados en partes iguales según un porcentaje determinado. Ejemplos de estas medidas son los cuartiles, deciles y percentiles.
¿Cuál es la diferencia principal entre cuartiles, deciles y percentiles?
-La principal diferencia radica en la cantidad de divisiones que hacen: los cuartiles dividen los datos en 4 partes iguales, los deciles en 10 partes iguales, y los percentiles en 100 partes iguales.
¿Cómo se calcula la posición de los cuartiles?
-La posición de los cuartiles se calcula con la fórmula (n / 4), donde n es el número total de datos en el conjunto. El valor obtenido nos indica la posición en la que se encuentra cada cuartil.
¿Qué representa el cuartil Q2?
-El cuartil Q2 corresponde a la mediana de un conjunto de datos. Es el valor que divide el conjunto en dos partes iguales y se calcula de forma similar al cuartil.
¿Por qué no hay cuatro cuartiles, sino solo tres?
-Aunque los cuartiles dividen los datos en cuatro partes iguales, solo existen tres cuartiles: Q1 (primer cuartil), Q2 (mediana), y Q3 (tercer cuartil).
¿Cómo se calculan los deciles?
-Para calcular los deciles, se utiliza la fórmula (k * n / 10), donde k es el número del decil (del 1 al 9), y n es el total de datos. Los deciles dividen el conjunto en 10 partes iguales, pero solo hay 9 deciles.
¿Qué es un percentil y cómo se calcula?
-Un percentil es un valor que divide un conjunto de datos en 100 partes iguales. Se calcula usando la fórmula (k * n / 100), donde k es el número del percentil (del 1 al 99) y n es el total de datos.
¿Qué es la fórmula para calcular los cuartiles, deciles y percentiles?
-La fórmula general para calcular estas medidas es: L + ((k * n / m) - F) * h, donde L es el límite inferior del intervalo, k es el número del cuartil, decil o percentil, n es el total de datos, m es el número de divisiones (4 para cuartiles, 10 para deciles, 100 para percentiles), F es la frecuencia acumulada del intervalo anterior y h es la amplitud del intervalo.
¿Qué sucede si no encontramos el valor exacto en la columna de frecuencias acumuladas?
-Si no encontramos el valor exacto en la columna de frecuencias acumuladas, se debe seleccionar el número inmediatamente superior al valor buscado y trabajar con los datos correspondientes a esa fila.
¿Cómo se calcula la amplitud del intervalo?
-La amplitud del intervalo se calcula restando el límite inferior del intervalo del límite superior. Por ejemplo, si el intervalo es de 30 a 40, la amplitud será 40 - 30 = 10.
Outlines

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифMindmap

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифKeywords

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифHighlights

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифTranscripts

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифПосмотреть больше похожих видео

Cuartiles, deciles y percentiles, datos agrupados, no agrupados, medidas de posición
Cuartiles, Deciles y Percentiles | Datos agrupados puntualmente

CUARTILES, DECILES Y PERCENTILES PARA DATOS NO AGRUPADOS

Conceptos estadísticos básicos

Cuartiles, deciles y percentiles Definición e interpretaciones
MEDIDAS DE POSICIÓN: PERCENTILES, DECILES Y CUARTILES #estadistica #deciles #percentiles
5.0 / 5 (0 votes)
