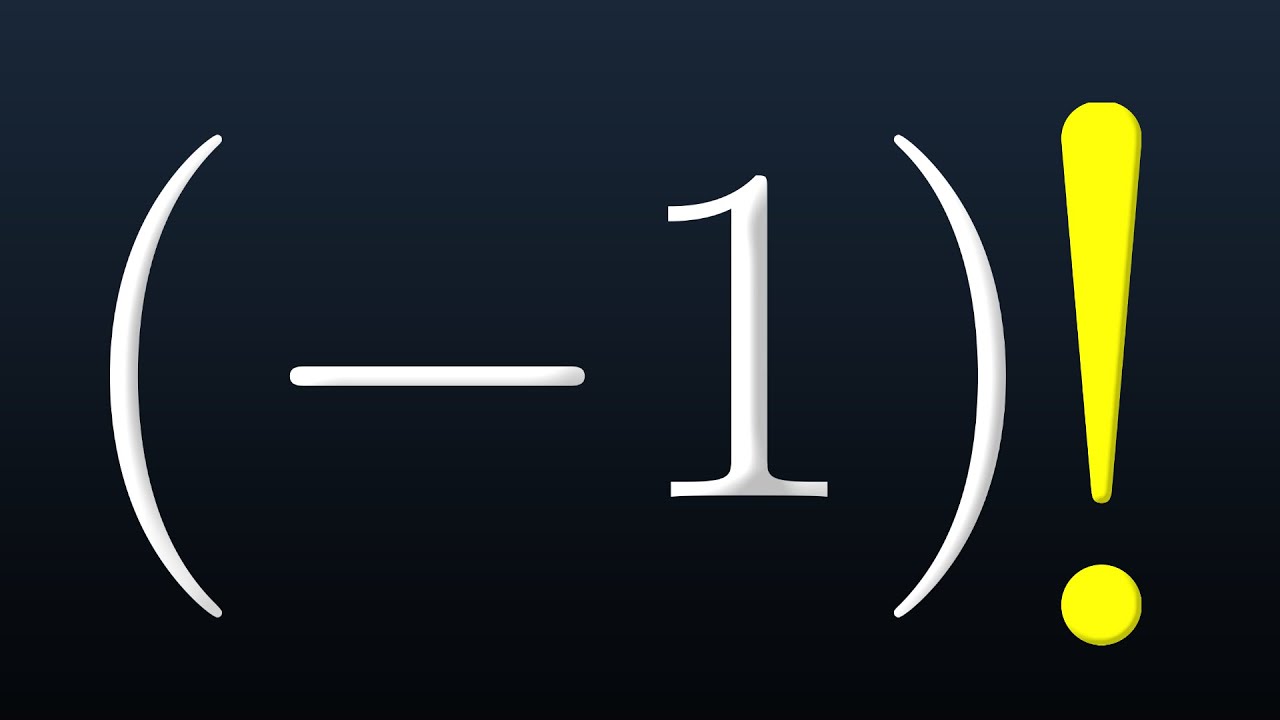Why is 0! = 1?

Summary

The video explores the concept of factorials, specifically the value of 0! being equal to 1, and connects this idea to broader mathematical concepts. The speaker uses relatable examples like powers of numbers and factorials to engage the audience. The discussion emphasizes the beauty of mathematics as an imagined world with consistent rules, showcasing how complex ideas like Fourier transforms and complex numbers emerged through curiosity, without an initial practical application in mind. Ultimately, the video celebrates the unexpected discoveries and the abstract nature of math that later finds real-world applications.

Takeaways

• 😀 0! equals 1 because it maintains consistency in the mathematical system, even though it may seem counterintuitive.
• 😀 Factorials can be thought of as a sequence of multiplying down from a given number, and this process works consistently even for 0!.
• 😀 When you look at factorials in reverse, dividing down from larger numbers to 1, the pattern suggests that 0! should equal 1.
• 😀 Mathematics is an imagined world with its own set of consistent rules, independent of practical application.
• 😀 The significance of mathematical concepts often emerges later, even if their initial discovery wasn’t focused on practical uses.
• 😀 Fourier’s work on wave functions showed that complex things, like wave patterns, can be broken down into simple sine functions.
• 😀 Fourier didn’t initially think of practical applications for his findings; they came later, but the mathematics remained useful.
• 😀 Just like in powers, you can go backward through the numbers in factorials, and it’s important that the rules remain consistent.
• 😀 The application of abstract mathematical ideas, such as complex numbers and wave functions, often surprises us in their real-world use.
• 😀 Mathematics doesn’t always need to have an immediate application; its value lies in its consistent logical system.
• 😀 The journey of discovering and understanding mathematical rules is as valuable as the practical outcomes they lead to.

Q & A

Why is 0! defined as 1?

0! is defined as 1 to maintain consistency in mathematical formulas. Factorials represent the product of integers down to 1, and since there are no integers below 1, defining 0! as 1 ensures that factorial-related formulas remain valid for all non-negative integers.

How does the analogy of powers help explain the concept of factorials?

The analogy of powers helps by showing how numbers grow when multiplied (for powers) and shrink when divided (for reverse powers). This reverse process mirrors how factorials can be divided step by step, where division by 2, 3, and 4 can be used to understand how factorials function, ultimately leading to the definition of 0! as 1.

What does the speaker mean by math being an 'imagined world'?

The speaker refers to math as an 'imagined world' to emphasize that mathematics operates within a consistent set of abstract rules, independent of practical applications. This conceptual framework allows mathematicians to explore ideas purely for the sake of exploration, without immediate concern for real-world utility.

How does the speaker view the relationship between abstract math and practical applications?

The speaker believes that while mathematics may begin as an abstract exploration (e.g., Fourier’s work with wave functions), its applications often emerge later in unexpected fields, like engineering or communications. This underscores the idea that the value of math lies in its logical consistency and not necessarily in its immediate practicality.

What role does the concept of 'wave functions' play in this discussion?

Wave functions are introduced as an example of mathematical curiosity that became widely applicable later, especially in fields like signal processing and communications. The speaker uses this to highlight how initially abstract mathematical ideas can have profound practical implications.

What is the significance of Fourier's discovery in the context of this discussion?

Fourier’s discovery that complex waveforms can be broken down into simpler sine functions is significant because it illustrates how abstract math (wave functions) can have practical applications, such as in electrical communications. This discovery shows the unexpected ways that pure mathematics can influence technology.

Why does the speaker argue that math doesn't need to have immediate practical use?

The speaker argues that math doesn't need immediate practical use because the essence of mathematics lies in its logical and consistent system of rules. These rules form an internally coherent framework that can lead to unexpected discoveries and applications in the future.

How does the speaker suggest we approach understanding concepts like 0! or factorials?

The speaker suggests that understanding concepts like 0! and factorials is less about immediate intuitive reasoning and more about accepting the definitions that make the system of mathematics consistent. For example, 0! is defined as 1 because it aligns with mathematical principles like combinatorics.

What is the connection between powers and factorials that the speaker points out?

The connection between powers and factorials lies in the idea of moving between multiplication and division. Powers show numbers increasing when multiplied, and factorials are a reverse process that can be understood through division, ultimately leading to consistent definitions like 0! = 1.

What does the speaker mean by saying math is 'meaningful'?

The speaker refers to math as 'meaningful' because it operates within a logical, consistent system of rules, regardless of whether its immediate application is clear. This internal consistency is what makes math significant and impactful in both theoretical and practical contexts.