[SER222] M02_02 Algorithm Analysis (3/3): What’s Next?
Summary
TLDREn este video, se discute la eficiencia del algoritmo de ordenamiento mergesort, destacando su complejidad de tiempo O(n log n) como la mejor posible para casos generales. Se plantea la pregunta de si es posible superar esta complejidad, y la respuesta es que no. El video prepara al espectador para una demostración del teorema de 'límite inferior', el cual prueba que no es posible crear un algoritmo de ordenamiento más rápido que O(n log n) en el caso general. Esta demostración se basa en la complejidad inherente del problema de ordenación.
Takeaways
- 😀 El algoritmo Mergesort tiene una complejidad temporal de O(n log n), lo que lo hace eficiente para ordenar.
- 😀 No es posible crear un algoritmo de ordenamiento más rápido que O(n log n) para el caso general.
- 😀 Mergesort y Quicksort son ejemplos de algoritmos de ordenamiento que tienen una complejidad temporal O(n log n).
- 😀 La afirmación de que O(n log n) es el límite inferior de la complejidad para el ordenamiento es un desafío matemático importante.
- 😀 El concepto de 'límite inferior' se refiere al mínimo trabajo necesario que cualquier algoritmo de ordenamiento debe realizar.
- 😀 Probar que O(n log n) es el límite inferior de la complejidad de ordenamiento requiere un análisis profundo del problema en sí, no solo de los algoritmos específicos.
- 😀 El objetivo es probar que no existe ningún algoritmo de ordenamiento que pueda ser más rápido que O(n log n) en cualquier escenario.
- 😀 Esta prueba debe ser válida independientemente de la implementación del algoritmo o el entorno en el que se ejecute.
- 😀 La prueba de límite inferior es compleja y generalmente no se realiza con frecuencia debido a la dificultad técnica que conlleva.
- 😀 En la siguiente sección del curso se dedicará tiempo a demostrar matemáticamente que no existe un algoritmo de ordenamiento mejor que O(n log n).
Q & A
¿Qué algoritmo de ordenación se menciona como ejemplo de tiempo O(n log n)?
-El algoritmo de ordenación mencionado como ejemplo de tiempo O(n log n) es el mergesort.
¿Es posible escribir un algoritmo de ordenación más rápido que O(n log n)?
-No, no es posible escribir un algoritmo de ordenación que sea más rápido que O(n log n) en el caso general de ordenación.
¿Cuál es la importancia de la demostración que se va a realizar en el video?
-La demostración que se va a realizar en el video tiene como objetivo probar el límite inferior de ordenación, es decir, que cualquier algoritmo de ordenación requiere al menos O(n log n) de tiempo.
¿Qué significa que la demostración sea sobre el 'problema en sí'?
-Significa que la prueba debe centrarse en las características inherentes del problema de ordenación, no en las implementaciones específicas de los algoritmos ni en los entornos de programación.
¿Por qué es complicado realizar una prueba de límite inferior para los algoritmos de ordenación?
-Es complicado porque una prueba de límite inferior debe demostrar que ningún algoritmo puede hacer menos trabajo que una cantidad específica, sin importar la plataforma o el tipo de algoritmo, lo cual es una afirmación fuerte y requiere una argumentación exhaustiva.
¿Qué significa que la prueba de límite inferior de ordenación deba ser válida para cualquier 'mundo' o contexto?
-Significa que la prueba debe ser general y aplicable en cualquier escenario, independientemente de los avances tecnológicos, los lenguajes de programación o los sistemas de computación, es decir, la prueba debe ser válida en cualquier época y contexto.
¿Cuál es el objetivo final de la prueba que se menciona en el video?
-El objetivo final de la prueba es demostrar que no existe un algoritmo de ordenación que sea más rápido que O(n log n), independientemente de las circunstancias.
¿Cómo se relaciona la complejidad O(n log n) con la eficiencia de los algoritmos de ordenación?
-La complejidad O(n log n) indica que el tiempo de ejecución de los algoritmos de ordenación, como mergesort y quicksort, aumenta proporcionalmente al número de elementos a ordenar, pero de manera más eficiente que los algoritmos que tienen una complejidad O(n^2).
¿Qué diferencia a los algoritmos como mergesort y quicksort de otros algoritmos de ordenación?
-Lo que diferencia a mergesort y quicksort es que ambos tienen una complejidad temporal O(n log n), lo que los hace mucho más eficientes que algoritmos como burbuja o inserción, que tienen una complejidad O(n^2).
¿Por qué se afirma que hacer una prueba de límite inferior es difícil?
-Porque implica demostrar que ningún algoritmo, en ninguna circunstancia o plataforma, puede superar una cierta barrera de tiempo, lo que requiere un razonamiento exhaustivo sobre el problema en su conjunto, no solo sobre algoritmos específicos.
Outlines

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифMindmap

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифKeywords

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифHighlights

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифTranscripts

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифПосмотреть больше похожих видео

[SER222] M02_02 The Algorithm (1/8): Practical Sorting

[SER222] M02_02 The Algorithm (8/8): Performance [v2]
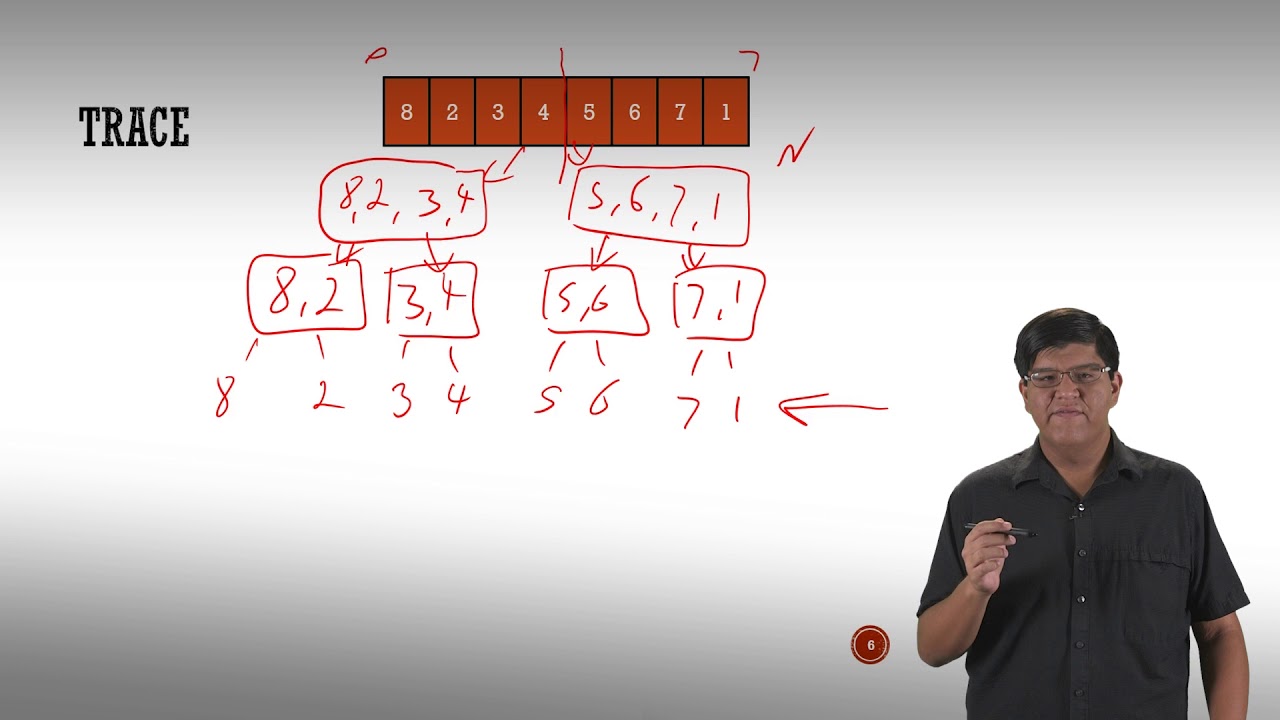
[SER222] M02_02 The Algorithm (4/8): Algorithm Trace

[SER222] M02_02 The Algorithm (5/8): Visual Trace

[SER222] M02_02 The Algorithm (6/8): Implementation

Notación Big O | Análisis de algoritmos de forma sencilla
5.0 / 5 (0 votes)
