El Péndulo Simple

Summary

En esta clase, el profesor Sergio Llanos explora el péndulo simple y su relación con el movimiento armónico simple. Se analizan conceptos clave como el período, la frecuencia y las fuerzas que actúan sobre la masa en un péndulo. A través de simulaciones y descomposición de fuerzas, se demuestra que el movimiento pendular puede ser considerado un movimiento armónico simple para ángulos pequeños. El video también incluye cálculos del período de oscilación y la tensión de la cuerda, proporcionando ejemplos prácticos. Los estudiantes son animados a comprender la conexión entre la teoría y la práctica en física.

Takeaways

• 😀 Un péndulo simple se compone de una cuerda fija que sostiene una masa, que oscila en un movimiento de va y viene.
• 😀 El periodo de un péndulo se define como el tiempo que toma realizar una oscilación completa.
• 😀 La frecuencia es el número de oscilaciones por unidad de tiempo, medida en Hertz.
• 😀 Las fuerzas que actúan sobre la masa en el péndulo son el peso (P) y la tensión de la cuerda (F).
• 😀 En un campo gravitacional, el peso se calcula como P = mg, donde m es la masa y g es la aceleración de la gravedad.
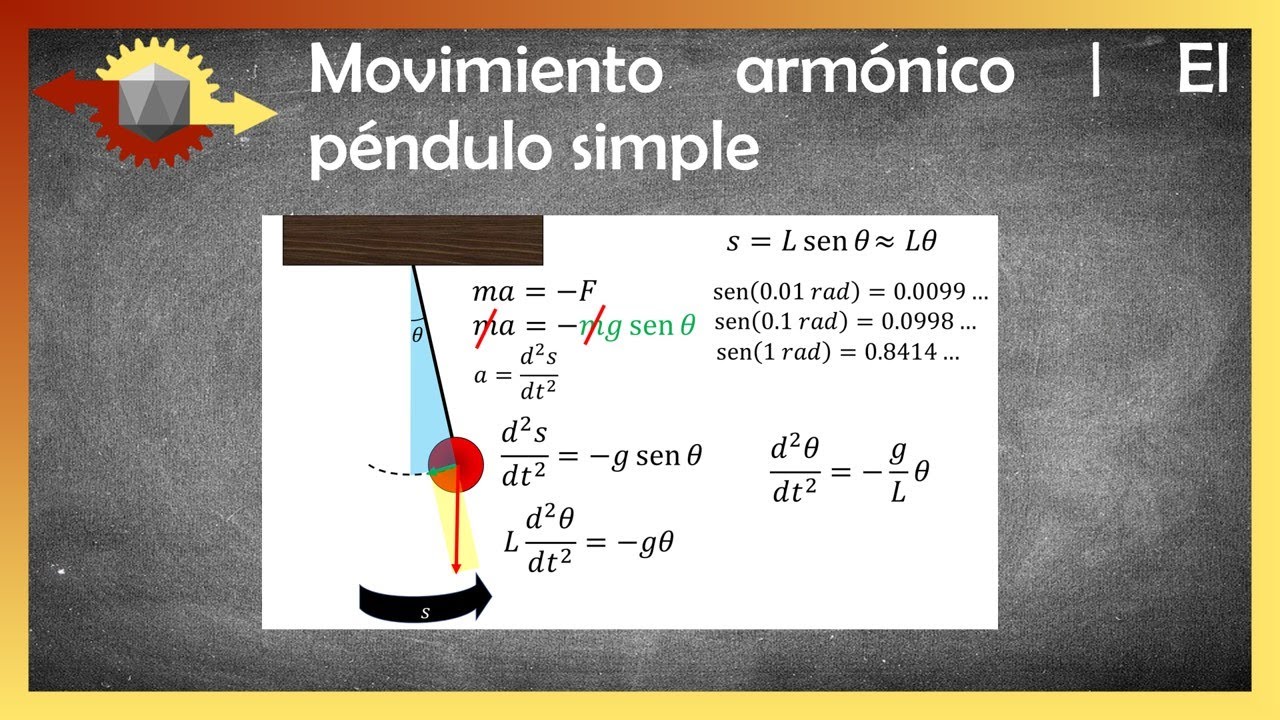
• 😀 La descomposición de fuerzas en un péndulo permite calcular las componentes tangencial y radial del peso utilizando trigonometría.
• 😀 Para ángulos pequeños (menos de 15 grados), el seno del ángulo se aproxima al mismo ángulo en radianes, lo que facilita los cálculos.
• 😀 La fuerza de restitución del péndulo, que causa su retorno a la posición de equilibrio, es proporcional al desplazamiento.
• 😀 La relación entre el periodo de un péndulo y su longitud es: T = 2π √(L/g), donde L es la longitud y g es la gravedad.
• 😀 La gravedad lunar afecta el periodo del péndulo; aunque el péndulo puede oscilar en la luna, su periodo será diferente debido a la menor gravedad.

Q & A

¿Qué es un péndulo simple?

Un péndulo simple es un sistema que consiste en una masa suspendida de una cuerda o varilla que oscila de un lado a otro debido a la gravedad.

¿Cuál es la relación entre el movimiento del péndulo y el movimiento armónico simple?

El movimiento del péndulo puede considerarse una aplicación del movimiento armónico simple, especialmente cuando se trabaja con ángulos pequeños, ya que la fuerza de restitución es proporcional al desplazamiento.

¿Qué se entiende por periodo en el contexto del péndulo?

El periodo es el tiempo que tarda el péndulo en completar una oscilación completa, es decir, en ir y volver al punto de partida.

¿Qué fuerzas actúan sobre la masa en el extremo del péndulo?

Las fuerzas que actúan sobre la masa son el peso (que actúa hacia abajo) y la tensión de la cuerda (que actúa hacia arriba).

¿Cómo se descomponen las fuerzas en un plano cartesiano?

Las fuerzas se descomponen en dos componentes: la componente radial (perpendicular al movimiento) y la componente tangencial (a lo largo del movimiento).

¿Por qué es importante trabajar con ángulos pequeños en el análisis del péndulo?

Es importante trabajar con ángulos pequeños porque para estos ángulos, el seno del ángulo en radianes es aproximadamente igual al propio ángulo, lo que simplifica las relaciones matemáticas.

¿Cómo se calcula la tensión en la cuerda del péndulo?

La tensión se calcula usando la relación T = mg coseno(θ), donde 'm' es la masa, 'g' es la aceleración de la gravedad y 'θ' es el ángulo con la vertical.

¿Cuál es la fórmula para el periodo de un péndulo en función de su longitud?

La fórmula para el periodo es T = 2π√(l/g), donde 'l' es la longitud del péndulo y 'g' es la aceleración de la gravedad.

¿Cómo afecta la longitud del péndulo a su periodo?

A medida que la longitud del péndulo aumenta, el periodo también aumenta; es decir, un péndulo más largo tarda más tiempo en completar una oscilación.

¿Qué sucede con el periodo de un péndulo si se encuentra en la luna?

El péndulo funcionará en la luna, pero su periodo será diferente debido a que la gravedad lunar es aproximadamente una sexta parte de la gravedad terrestre, lo que incrementará el periodo.