Ecuaciones factorizables
Q & A
Что такое факторизация уравнений?
-Факторизация уравнений — это процесс разложения уравнений на множители, то есть на несколько выражений, которые умножаются друг на друга, чтобы восстановить исходное уравнение.
Какую роль играет равенство уравнения нулю при факторизации?
-При факторизации уравнение должно быть равно нулю. Это необходимо для того, чтобы найти корни уравнения, так как уравнение можно разложить на множители только в случае, если оно приравнено к нулю.
Какие виды факторизации встречаются в алгебре?
-В алгебре существует несколько видов факторизации, включая факторизацию разности квадратов, разности кубов, а также преобразование в полные квадраты и другие стандартные методы.
Что происходит, если уравнение не равно нулю?
-Если уравнение не равно нулю, необходимо привести его к виду, в котором одна из сторон будет равна нулю. Это делается путем перемещения всех членов уравнения на одну сторону.
Что такое разность квадратов и как ее можно факторизовать?
-Разность квадратов — это выражение вида a² - b², которое можно факторизовать как (a + b)(a - b). Этот метод широко используется для факторизации уравнений.
Как факторизовать выражение вида x⁴ - 4?
-Для факторизации выражения x⁴ - 4 сначала нужно привести его к разности квадратов, поскольку x⁴ - 4 = (x² + 2)(x² - 2). Это позволяет найти два множителя, которые могут быть использованы для дальнейшего анализа уравнения.
Какие шаги нужно предпринять при факторизации уравнения x⁴ - 4 = 0?
-Сначала необходимо привести уравнение к виду, в котором оно равно нулю, например x⁴ - 4 = 0. Затем можно разложить это выражение на множители, используя разность квадратов, что дает (x² + 2)(x² - 2). После этого уравнение можно решить для x.
Как можно факторизовать уравнение с использованием квадратных корней?
-Для факторизации уравнений с использованием квадратных корней, сначала нужно извлечь корни из каждого из членов уравнения. Например, из x⁴ извлекается x², что позволяет упростить выражение и привести его к более удобному виду для дальнейшего решения.
Что такое полный квадрат и как он используется при факторизации?
-Полный квадрат — это выражение вида a² + 2ab + b², которое можно факторизовать как (a + b)². Этот метод используется для упрощения и разложения более сложных выражений на множители.
Какие ошибки можно допустить при факторизации уравнений?
-Одна из основных ошибок — это неверное использование методов факторизации, например, если уравнение не приравняно к нулю. Также важно правильно учитывать все знаки и правильно применять свойства разности квадратов и других типов факторизации.
Outlines

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифMindmap

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифKeywords

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифHighlights

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифTranscripts

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифПосмотреть больше похожих видео

0. ¿Qué es una Ecuación Diferencial? Tipos de ecuaciones diferenciales, solución de ED

Sistema de Ecuaciones 2x2 - Método de Eliminación o Reducción

DEFINICIÓN DE SISTEMAS DE ECUACIONES LINEALES
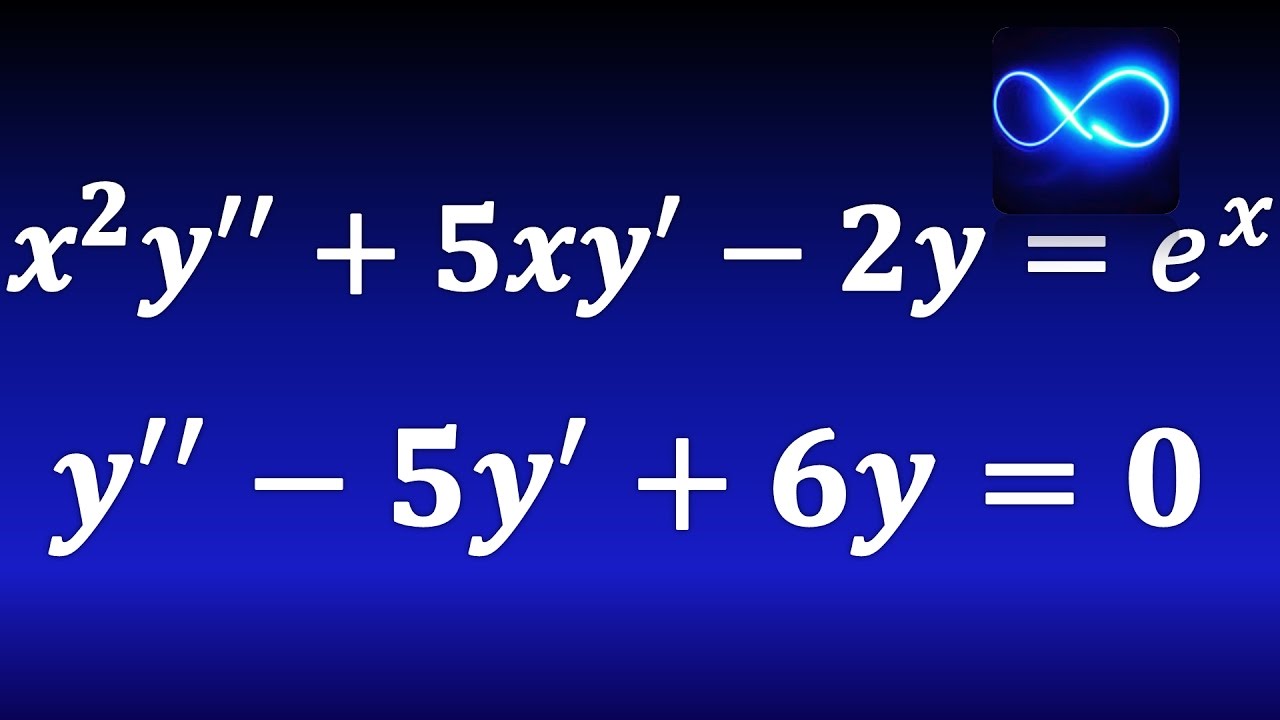
78. Qué son las ecuaciones de segundo orden, ecuaciones homogéneas y de coeficientes constantes

¿Qué aprenderás en el curso de ecuaciones polinómicas?

09. ¿Qué es un sistema de ecuaciones lineales con dos incógnitas?

Las 8 ecuaciones más importantes de la Física
5.0 / 5 (0 votes)