1. Ecuación diferencial de variables separables
Summary
TLDREn este vídeo tutorial de 'Mate Fácil', se resuelve una ecuación diferencial separable paso a paso. Se explica cómo separar las variables y manipular la ecuación para integrar ambos lados, obteniendo una solución en términos de una constante por x. Luego, se despeja la variable y se verifica la solución sustituyendo en la ecuación original. Se anima a los espectadores a practicar resolviendo ecuaciones similares y se invita a dejar comentarios para dudas o sugerencias.
Takeaways
- 📘 La ecuación diferencial que se resuelve es una ecuación separable.
- 🔄 Se reescribe la ecuación para separar las variables, colocando todas las 'x' en un lado y todas las 'y' en el otro.
- ✏️ Se utiliza la propiedad de que 'y' prima (la derivada de 'y') es igual a 'y' dividido por 'x'.
- 🔄 Se multiplica por 'x' para alinear los términos y se obtiene una nueva ecuación.
- 🧮 Se integran ambos lados de la ecuación para encontrar la función 'y'.
- 📐 Se recuerdan las integrales inmediatas para resolver la ecuación, utilizando el logaritmo natural.
- 📉 Se despeja la constante de la ecuación para encontrar 'y' en función de 'x'.
- 🔢 Se menciona que las constantes resultantes pueden ser cualquier número y se les puede asignar una sola constante para simplificar.
- 🔄 Se pasa el logaritmo natural al otro lado de la ecuación como una exponencial para despejar a 'y'.
- ✅ Se verifica la solución sustituyendo la función 'y' en la ecuación diferencial original y se confirma que la solución es correcta.
- 📚 Se invita a los espectadores a practicar resolviendo ecuaciones diferenciales similares para mejorar su comprensión.
Q & A
¿Qué tipo de ecuación diferencial se resuelve en el vídeo?
-Se resuelve una ecuación diferencial separable.
¿Cómo se identifica una ecuación diferencial como separable?
-Una ecuación diferencial es separable si se puede organizar de tal manera que todas las variables 'x' están en un lado y todas las variables 'y' en el otro lado.
¿Qué significa 'y prima' en el contexto del vídeo?
-'y prima' representa la derivada de la función 'y' con respecto a 'x'.
¿Cómo se convierte 'y prima' en una fracción en el vídeo?
-Se escribe 'y prima' como 'dy/dx', la cual se interpreta como una fracción donde 'dx' es el denominador.
¿Cuál es la estrategia para separar las variables en la ecuación diferencial mostrada?
-Se multiplica todo lo que está a la derecha por 'dx' y se pasa todo lo que está a la izquierda por 'dy', para que las 'x' queden en un lado y las 'y' en el otro.
¿Qué operaciones se realizan después de separar las variables?
-Se integran ambos lados de la ecuación, lo que implica encontrar las integrales inmediatas de 'dy/y' y 'dx/x'.
¿Cuál es la integral inmediata de 'dy/y'?
-La integral inmediata de 'dy/y' es 'ln|y| + C1', donde 'C1' es una constante de integración.
¿Cómo se despeja 'y' en la solución obtenida en el vídeo?
-Se isola 'y' eliminando las constantes del lado derecho de la ecuación y utilizando las propiedades de los logaritmos.
¿Qué significa 'despejar y' en el contexto de la solución de ecuaciones diferenciales?
-Despejar 'y' significa aislar 'y' en el lado izquierdo de la ecuación para obtener una expresión que represente la solución.
¿Cómo se verifica que la solución obtenida es correcta?
-Se verifica sustituyendo la solución en la ecuación diferencial original y asegurándose de que los dos lados de la ecuación sean iguales.
¿Cuál es la importancia de hacer ejercicios al final de cada vídeo mencionada en el guion?
-La importancia de hacer ejercicios es para que los estudiantes prueben y apliquen lo que han aprendido, lo que ayuda a fortalecer su comprensión y habilidades para resolver ecuaciones diferenciales.
Outlines

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифMindmap

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифKeywords

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифHighlights

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифTranscripts

Этот раздел доступен только подписчикам платных тарифов. Пожалуйста, перейдите на платный тариф для доступа.
Перейти на платный тарифПосмотреть больше похожих видео
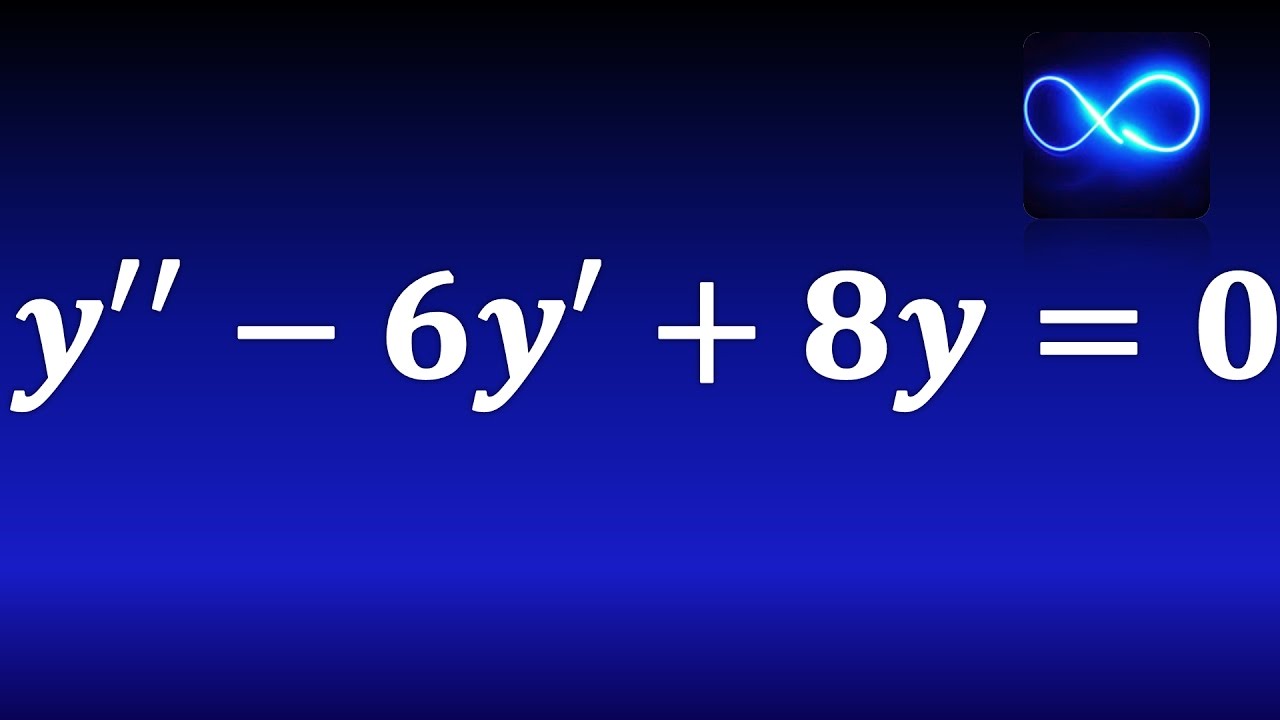
86. Ecuación diferencial de coeficientes constantes (segundo orden, homogénea) EJERCICIO RESUELTO
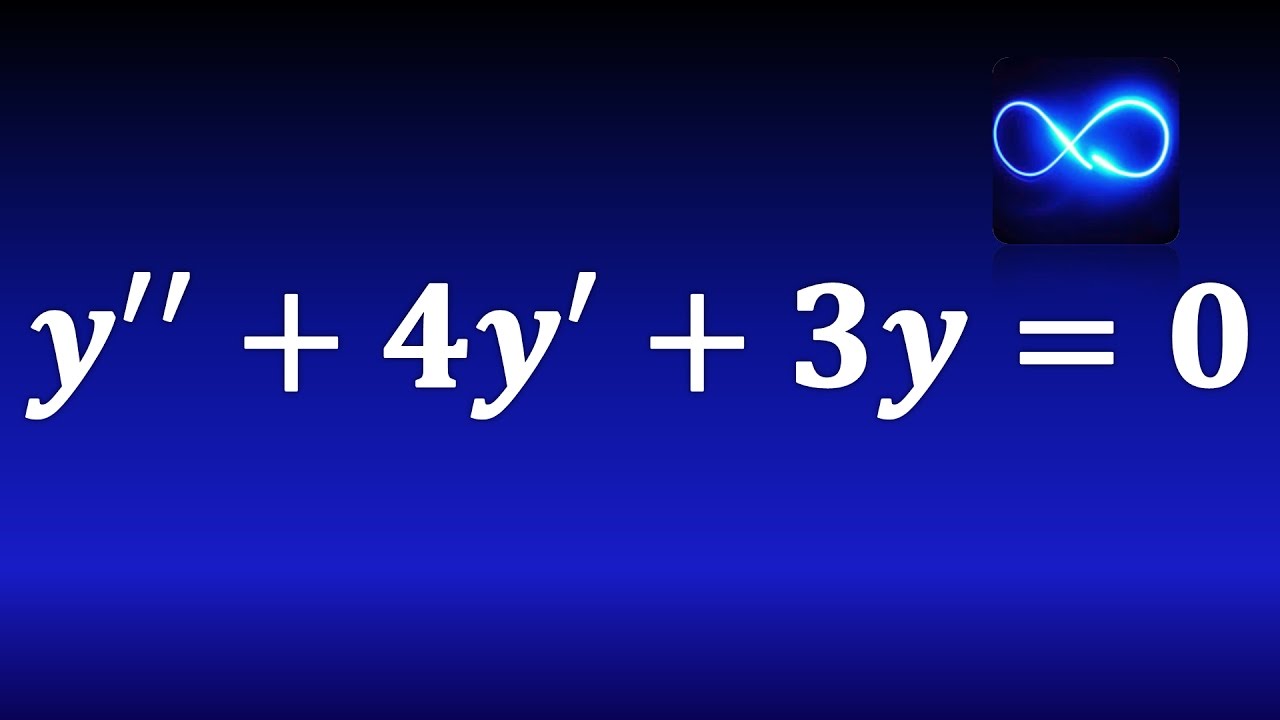
87. Ecuación diferencial de coeficientes constantes (segundo orden, homogénea) EJERCICIO RESUELTO
Simulación de sistema masa resorte amortiguador en SciLab.

06. Límite con indeterminación 0/0

01. Modelo simple de población, Ecuaciones Diferenciales

07. Valor de una función con valor absoluto
5.0 / 5 (0 votes)
