Área de un paralelogramo con Vectores
Summary
TLDREn este ejercicio, el objetivo es calcular el área de un paralelogramo en 3D, utilizando los vértices dados. Se explican los pasos para determinar los vectores que forman las aristas del paralelogramo, calculando el producto cruzado de dichos vectores para encontrar el área. A lo largo del proceso, se realizan diversas explicaciones sobre cómo obtener las componentes de los vectores y aplicar la regla del determinante para calcular el producto cruzado. Finalmente, se obtiene el módulo de este producto cruzado, lo cual proporciona el área deseada en unidades cuadradas.
Takeaways
- 😀 El ejercicio trata sobre el cálculo del área de un paralelogramo en 3D usando los vértices dados.
- 😀 Se utiliza el producto cruzado de dos vectores para encontrar el área del paralelogramo.
- 😀 Los vectores se obtienen restando las coordenadas de los puntos extremos de los vectores.
- 😀 Se calcula el producto cruzado entre los dos vectores para encontrar un tercer vector perpendicular.
- 😀 La magnitud del producto cruzado da como resultado el área del paralelogramo.
- 😀 Se realiza el cálculo de la magnitud del vector resultante utilizando la fórmula de la raíz cuadrada de la suma de los cuadrados de sus componentes.
- 😀 La magnitud del producto cruzado es la raíz cuadrada de 446, lo que da aproximadamente 21.1 unidades cuadradas.
- 😀 Se detallan las coordenadas de los puntos en el espacio 3D, como el punto (-2, -11), (2, 1, 2), entre otros.
- 😀 El cálculo utiliza la regla de determinantes para realizar el producto cruzado.
- 😀 El área final se presenta como una cantidad sin unidades específicas, pero se sugiere que podría ser en metros cuadrados si fuera el caso de una situación del mundo real.
Q & A
¿Qué se busca calcular en este ejercicio?
-En este ejercicio se busca calcular el área de un paralelogramo formado por tres vértices en un sistema de coordenadas tridimensional.
¿Cuáles son los vértices proporcionados en el ejercicio?
-Los vértices proporcionados son: A (-2, -1, 2), B (1, -2, 3), y C (-1, 2, -3).
¿Qué método se utiliza para calcular el área del paralelogramo?
-El método utilizado para calcular el área del paralelogramo es el producto cruzado de los vectores que forman el paralelogramo.
¿Qué son los vectores involucrados en el cálculo del área?
-Los vectores involucrados son el vector v formado por los vértices A y el origen, y el vector w formado por los vértices B y el origen.
¿Cómo se obtiene el primer vector v?
-El primer vector v se obtiene restando las coordenadas del origen (0, 0, 0) de las coordenadas del vértice A (-2, -1, 2), lo que da el vector v = (-2, -1, 2).
¿Cómo se obtiene el segundo vector w?
-El segundo vector w se obtiene restando las coordenadas del origen (0, 0, 0) de las coordenadas del vértice B (1, -2, 3), lo que da el vector w = (1, -2, 3).
¿Cómo se calcula el producto cruzado de los dos vectores?
-El producto cruzado se calcula utilizando la fórmula de determinantes para un producto cruzado de tres componentes. El resultado es un vector cuyas componentes se obtienen mediante determinantes.
¿Qué es el determinante utilizado en el cálculo del producto cruzado?
-El determinante utilizado es una matriz 3x3 que tiene como filas los vectores unitarios i, j, k y las componentes de los vectores v y w.
¿Cuál es el resultado del producto cruzado de los vectores v y w?
-El resultado del producto cruzado es el vector (1, 8, 5), lo que representa la magnitud y dirección del paralelogramo formado por los dos vectores.
¿Cómo se calcula el área del paralelogramo a partir del producto cruzado?
-El área del paralelogramo se calcula tomando la magnitud del vector resultante del producto cruzado, que es la raíz cuadrada de la suma de los cuadrados de sus componentes. En este caso, el área es aproximadamente 9.49 unidades cuadradas.
Outlines

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードMindmap

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードKeywords

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードHighlights

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードTranscripts

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレード関連動画をさらに表示

ÁREA DE UN POLIGONO EN EL PLANO CARTESIANO
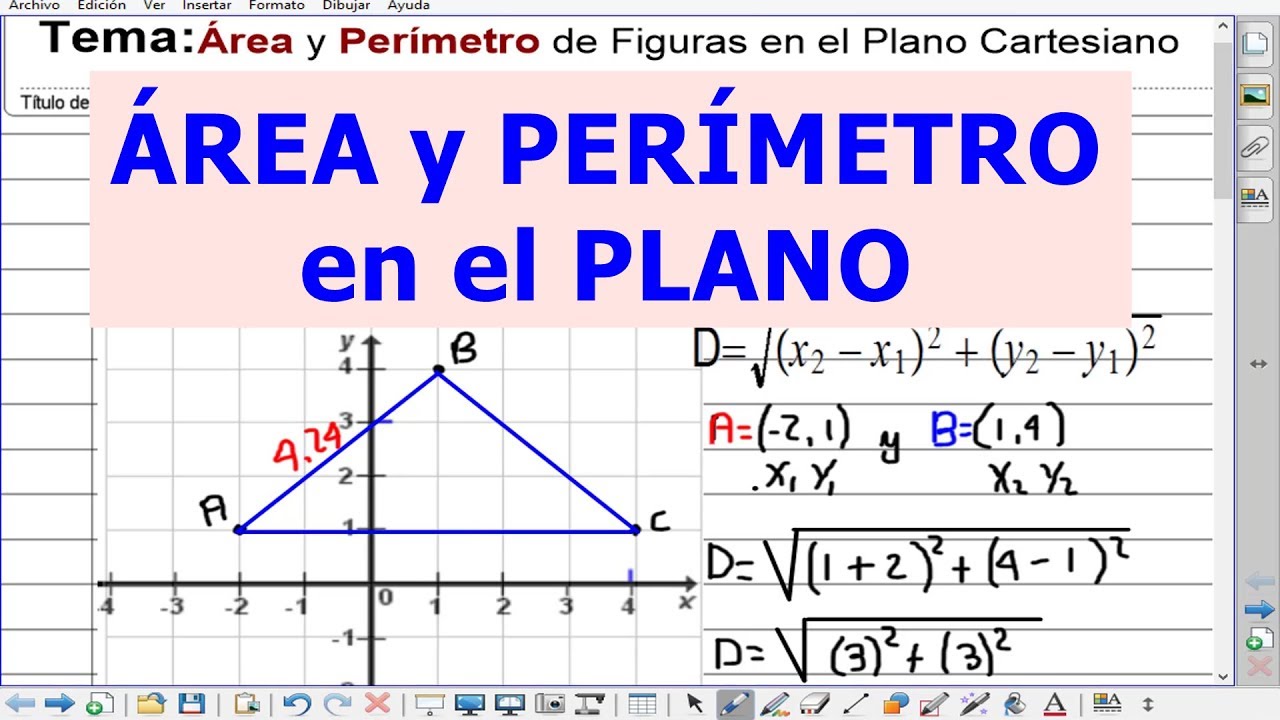
Área y Perímetro de Figuras en el Plano Cartesiano.

Geometría Analítica: Vértice de un triangulo, con analítica

Método: rectángulos CIRCUNSCRITOS | Área bajo la curva | Cálculo Integral

40. Programación desde Cero | Ciclos | Ejercicio 1 - Suma de los N primeros números

Límite con teorema del encaje 1
5.0 / 5 (0 votes)
