Materi Transformasi Fourier - MK Matematika Radiologi

Summary

In this video, Atika explains the concept of Fourier Transform and its application in signal processing, particularly in digital image processing, such as in CT scans and MRIs. She introduces the idea of digital images as signals, emphasizing the importance of transforming signals from the time domain to the frequency domain for easier analysis, such as filtering. Atika covers the history of Fourier Transform, its mathematical foundation, and how it can be applied to complex signals like square waves. The video provides insight into how this transformation is used to simplify the analysis of signals in various digital applications.

Takeaways

• 😀 The script discusses the concept of 'transformasi foye,' which is related to the transformation of signals from the time domain to the frequency domain, making signal processing more practical.
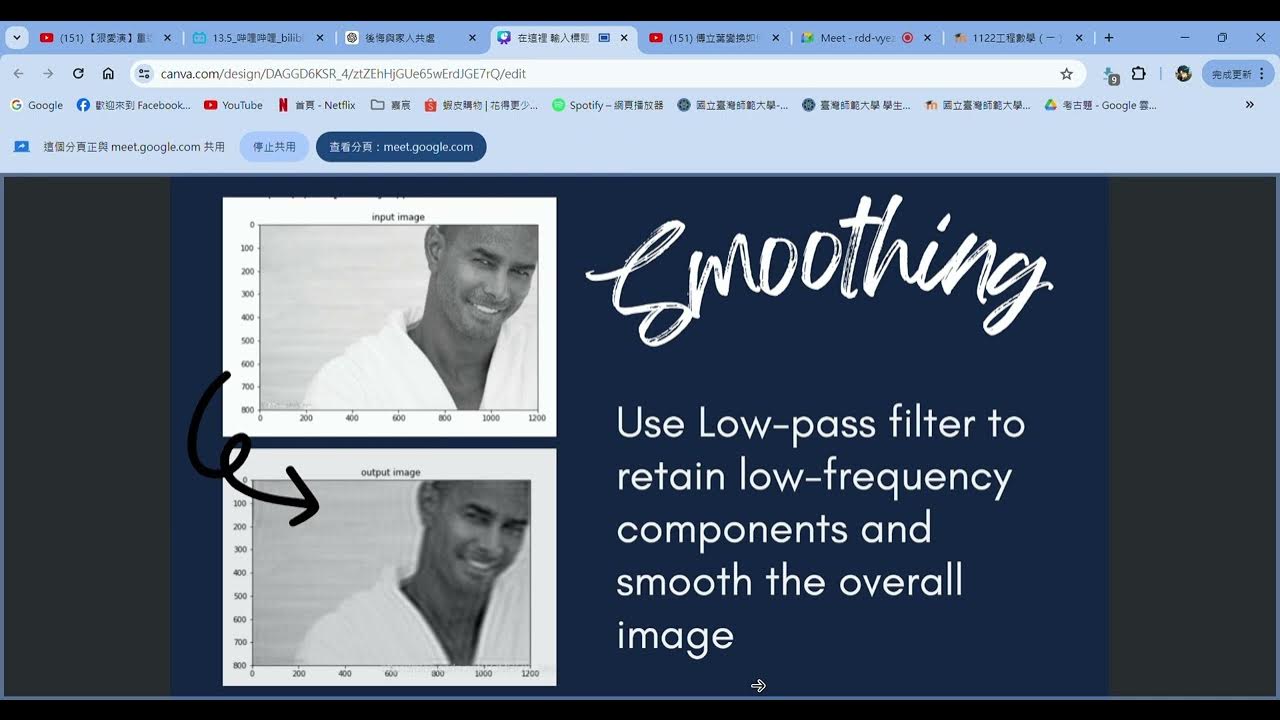
• 😀 The content covers digital image processing and signal analysis, particularly in the context of computer tomography (CT), MRI, and similar technologies.
• 😀 Digital images, like JPEG and BMP formats, are examples of signals, which can be processed to enhance analysis and visualization.
• 😀 The definition of a signal is presented as any measurable energy in space and time, and its transformation can improve processing efficiency.
• 😀 Transforming signals into the frequency domain allows for more practical signal processing, such as filtering, which makes it easier to analyze complex signals.
• 😀 The Radon transformation is explained as a method to transform signals from the spatial domain (position-based) into a time-based function.
• 😀 The history of Fourier transformation is introduced, with Fourier's discovery in 1822 that periodic functions can be expressed as sums of sinusoidal functions (sine and cosine).
• 😀 The transformation process is explained using the concept of periodic functions, where signals are represented as sinusoidal waves with different frequencies.
• 😀 The Fourier series expansion is covered, with emphasis on how complex signals can be approximated by summing simpler sinusoidal functions with different frequencies and amplitudes.
• 😀 The script introduces mathematical formulas for Fourier series, explaining the relationship between the time and frequency domains in signal analysis, including the general formula for Fourier transforms.

Q & A

What is the main topic discussed in the transcript?

The main topic discussed is the transformation of signals, particularly focusing on Radon transformation and Fourier transformation, and their application in digital image processing, such as in computer tomography (CT) and MRI.

What is the significance of digital images in the context of signal processing?

Digital images, like JPEG and BMP, are signals that can be processed to improve analysis and visualization. Signal processing helps in extracting meaningful information by transforming signals into a more practical domain, such as frequency domain.

How does signal transformation benefit the analysis of signals?

Signal transformation allows the signal to be moved from the time domain to the frequency domain, making processes like filtering more efficient. This facilitates clearer analysis and manipulation of the signal.

What is the role of Fourier Transformation in signal processing?

Fourier Transformation converts signals from the time domain into the frequency domain. This allows for the representation of periodic signals as sums or integrals of sinusoidal functions (sine and cosine), making it easier to analyze and process complex signals.

Who discovered Fourier Transformation and when?

Fourier Transformation was discovered by Jean-Baptiste Joseph Fourier in 1822. He demonstrated that periodic functions could be expressed as sums of sine and cosine functions of various frequencies.

What are periodic functions, and why are they important in signal processing?

Periodic functions repeat at regular intervals. In signal processing, periodic functions can be decomposed into sine and cosine components, making them easier to analyze and manipulate, especially for filtering and other operations.

Can you explain the graphical representation of a periodic function using sine and cosine?

The periodic function can be visualized by drawing a circle where a point moves counterclockwise. This movement is used to represent the sine and cosine waves. The sine wave represents vertical movement, and the cosine wave represents horizontal movement, both of which help describe the periodic signal.

What is the process of converting time-domain signals to frequency-domain signals using Fourier Transform?

To convert a time-domain signal to a frequency-domain signal, the Fourier Transform uses mathematical formulas involving sinusoidal functions. This results in the signal being represented in terms of frequency rather than time, enabling more efficient analysis.

How does Fourier series help in approximating complex signals?

The Fourier series decomposes complex signals into a sum of sinusoidal functions (sine and cosine) with different frequencies and amplitudes. By using more terms in the series, the approximation becomes more accurate, allowing for the reproduction of complex signals from simple sinusoidal components.

What is the inverse Fourier Transform, and how is it used?

The inverse Fourier Transform is a process that converts a signal from the frequency domain back into the time domain. It uses a formula that integrates the frequency-domain signal with an exponential factor to recover the original time-domain signal.