Control System Input Signals (Step, Ramp, Parabolic, Noise, Rectangular, Impulse, and Sinusoidal)
Summary
TLDRIn this video, the presenter discusses various input signals used in process models and control systems, illustrating their importance for testing control system performance. The video covers input signals such as step, ramp, parabolic, noisy, rectangular pulse, impulse, and sinusoidal signals, each explained with an example of a water bucket system. The presenter also introduces the Laplace transforms of each signal and mentions additional resources for further learning. This overview is designed to help viewers understand the role of different input signals in modeling and system behavior analysis.
Takeaways
- 😀 A process model is typically represented by a block diagram that shows input-output relationships, like modeling a water bucket being filled.
- 😀 The input signal is what we apply to a system, and the output is the resulting system behavior, such as the height of water in a bucket.
- 😀 Different input signals allow us to test and evaluate the performance of a control system, which is why they're often called standard test inputs.
- 😀 A step input signal represents an instantaneous change in input, similar to turning on a light switch, and its Laplace transform is a/a.
- 😀 A ramp input signal steadily increases over time, akin to gradually increasing water flow into the bucket, with its Laplace transform being the slope of the ramp divided by s².
- 😀 A parabolic input grows quadratically over time, and its Laplace transform is also presented in the script for reference.
- 😀 Noisy input signals have no predictable pattern and are usually undesirable, making them difficult to work with in control systems.
- 😀 A rectangular pulse input is like a step input that turns off after a given period, such as turning the tap on for three seconds and then off, with its Laplace transform presented.
- 😀 An impulse input is a very short, intense surge of input, represented by a Dirac delta function, and its Laplace transform is 1.
- 😀 A sinusoidal input signal fluctuates in a sine wave pattern, and its Laplace transform is also included in the script for further analysis.
- 😀 The video offers insights into these standard input signals and their corresponding Laplace transforms, which help in analyzing and validating control system responses.
Q & A
What is the purpose of input signals in process modeling?
-Input signals allow us to test and evaluate the performance of a control system. They are used to study how the system reacts to different types of inputs, which helps in understanding its behavior under various conditions.
What does the process model represent in a system?
-The process model represents the relationship between the input and output of a system. In the example of a water bucket, the process model shows how the height of the water changes based on the amount of water coming in (input).
What is a step input signal, and how is it represented?
-A step input signal is like flipping a light switch on. At a specified time, the input jumps from zero to a set value, and the system reacts to this sudden change. Mathematically, it is represented as a jump from 0 to 1 at time zero.
What is the Laplace transform of a step input signal?
-The Laplace transform of a step input signal is represented as A/s, where A is the magnitude of the input.
How does a ramp input signal behave, and how is it represented?
-A ramp input signal grows progressively over time at a constant slope. It starts at zero at time zero and increases linearly. In the bucket example, this would be like slowly opening the tap over time. Mathematically, it is represented as a line with a constant slope.
What is the Laplace transform of a ramp input signal?
-The Laplace transform of a ramp input signal is the slope of the ramp divided by s squared.
What is a parabolic input signal, and how is it represented?
-A parabolic input signal grows quadratically with time, forming a curve. It increases faster than a ramp input. The mathematical representation of this input is a quadratic function.
What is a noisy input signal, and why is it undesirable?
-A noisy input signal has no clear pattern and is typically unpredictable. It is undesirable because it introduces uncertainty into the system, making it difficult to analyze or control effectively.
What is a rectangular pulse input signal, and how does it differ from a step input?
-A rectangular pulse input signal is similar to a step input but only lasts for a fixed duration before turning off. It is like turning the tap on full for a specific period and then turning it off again.
What is an impulse input signal, and why is it considered theoretical?
-An impulse input signal is a theoretical concept where the input is extremely high at a single instant of time, but zero at all other times. It is often referred to as the Dirac delta function and is used to approximate a sudden, very brief event like a lightning bolt.
What is a sinusoidal input signal, and how is it represented?
-A sinusoidal input signal oscillates in a sine wave pattern, commonly used to represent periodic signals. Mathematically, it is represented as a sine or cosine function.
What is the Laplace transform of a sinusoidal input signal?
-The Laplace transform of a sinusoidal input signal is a more complex expression involving frequency components, typically represented in terms of a complex exponential function.
Outlines

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードMindmap

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードKeywords

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードHighlights

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードTranscripts

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレード関連動画をさらに表示
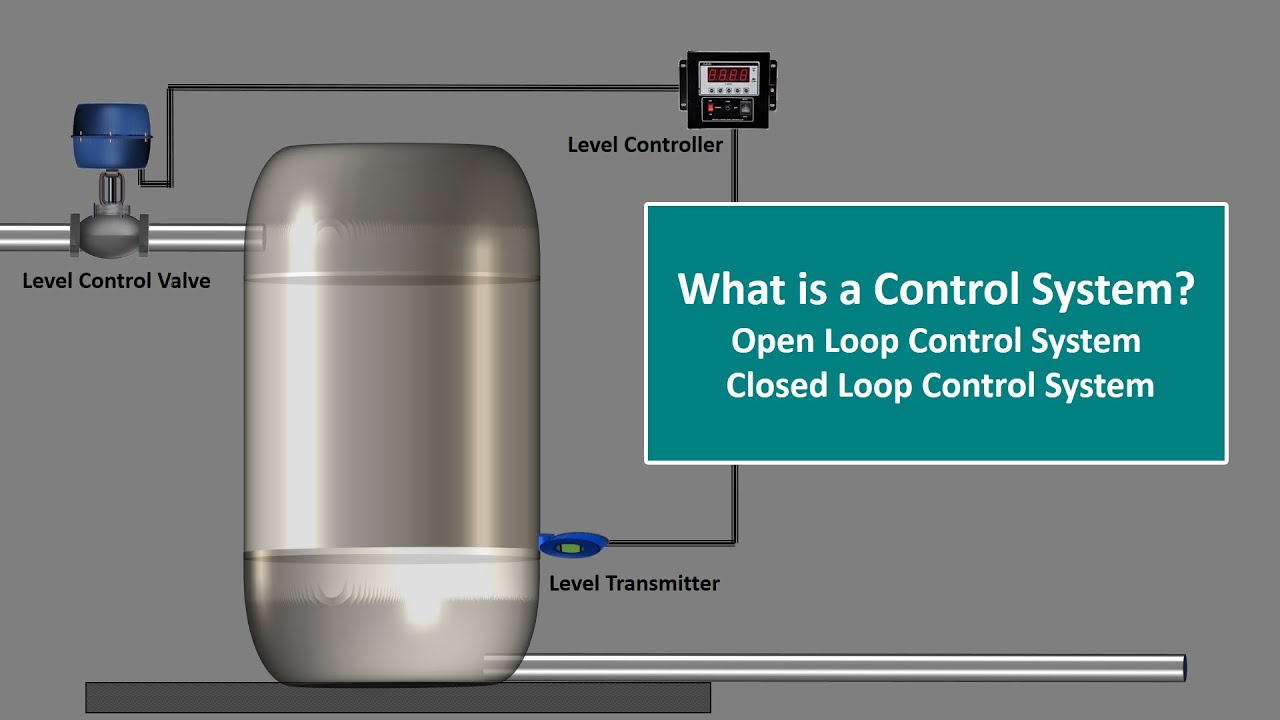
What is Control System.Control System Engineering.Open Loop and Closed Loop Control System.Explained
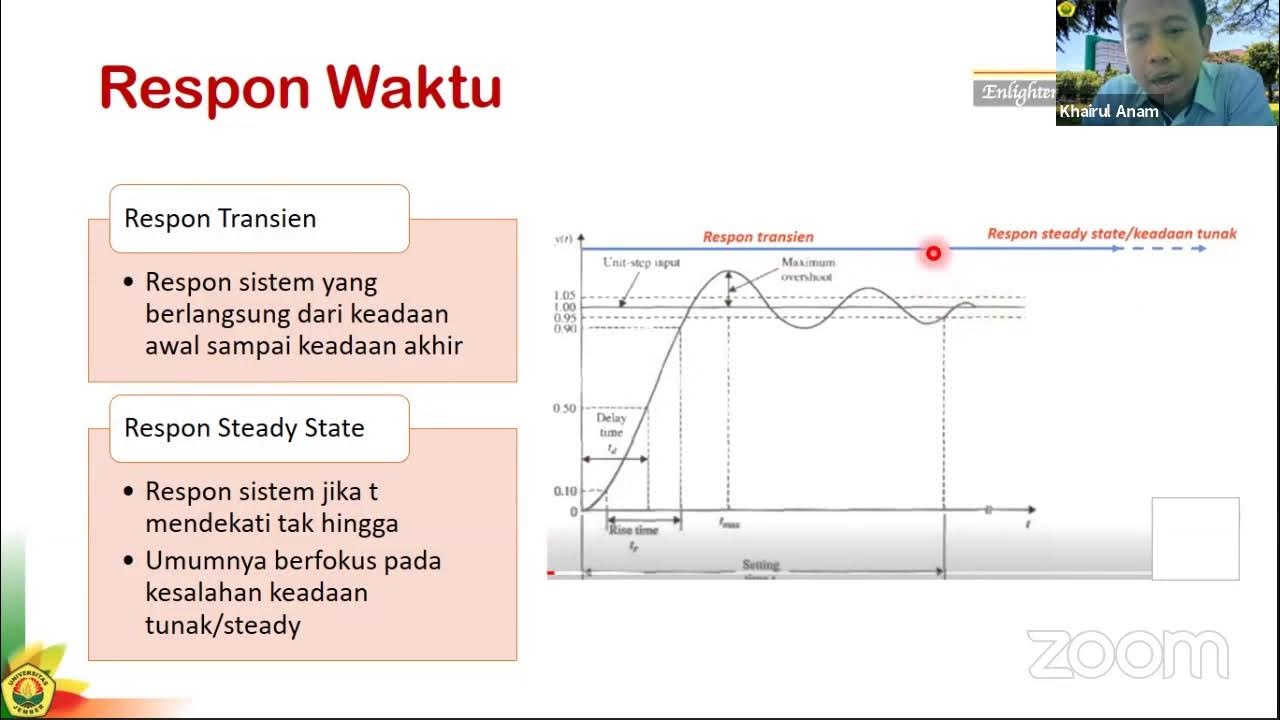
Sistem Kontrol #3a: Analisis Repon Sistem - Pendahuluan

What are Transfer Functions? | Control Systems in Practice

03. MG3217 Kendali Proses S01: Respons Sistem Orde - 1

Pertemuan 3. Sistem Kendali Pada Robot | Robotic and Control System

Pengantar Teknik Robotika 6 - Pengantar Sistem Kendali
5.0 / 5 (0 votes)
