KERUCUT
Summary
TLDRThis educational video teaches about cones, focusing on their volume and surface area. The script begins by introducing the concept of a cone and explores its properties, such as the base and slant height. The volume formula is derived and explained as 1/3 πr²h, with examples demonstrating how to calculate it. It then covers the surface area, showing how to calculate both the base and slant surface areas. The video also provides real-world examples, like calculating the surface area of a conical hat and a few challenging exercises. The lesson is presented with clear explanations and step-by-step problem-solving techniques.
Takeaways
- 😀 Cones have a circular base and a slanted side, known as the cone's surface or slant height.
- 😀 The volume of a cone can be calculated using the formula: 1/3 × π × r² × h, where r is the radius and h is the height of the cone.
- 😀 The relationship between the radius (r), height (h), and slant height (s) of a cone is given by the Pythagorean theorem: r² + h² = s².
- 😀 The surface area of a cone is the sum of the area of its circular base (π × r²) and the area of its slanted surface (π × r × s).
- 😀 The slant height of a cone can be calculated using the Pythagorean theorem when the radius and height are known.
- 😀 A cone's surface area formula is derived from the relationship between the slanted surface and the base's circle.
- 😀 To calculate the slanted surface area, use the formula: 2 × π × r × s, where r is the radius and s is the slant height.
- 😀 In practical examples, the volume and surface area of cones can be solved by applying the correct formulas and substituting the given values.
- 😀 In problems involving cones, sometimes the slant height (s) is not directly given, and you must calculate it using the Pythagorean theorem.
- 😀 The example of calculating the volume and surface area of a cone involves using π = 3.14 or 22/7, depending on the given problem context.
Q & A
What is the main topic of the lesson discussed in the video?
-The main topic is about cones, specifically focusing on the volume and surface area of a cone.
What is the formula to calculate the volume of a cone?
-The formula to calculate the volume of a cone is 1/3 * π * r² * h, where r is the radius of the base and h is the height of the cone.
What is the relationship between the slant height (s), radius (r), and height (h) of a cone?
-The relationship between the slant height (s), radius (r), and height (h) of a cone is given by the Pythagorean theorem: s² = r² + h².
How is the surface area of a cone calculated?
-The surface area of a cone is the sum of the area of the circular base (π * r²) and the lateral surface area (π * r * s), where r is the radius and s is the slant height.
What is the formula for the lateral surface area (slant surface) of a cone?
-The formula for the lateral surface area of a cone is π * r * s, where r is the radius and s is the slant height.
What does 'slant height' refer to in a cone?
-The slant height refers to the distance from the top of the cone to any point on the perimeter of the base, along the side of the cone.
How do you calculate the slant height if it is not provided?
-The slant height can be calculated using the Pythagorean theorem: s = √(r² + h²), where r is the radius and h is the height of the cone.
What is the relationship between the sector area and the total area of a circle when calculating the lateral surface area of a cone?
-The sector area of the cone is a fraction of the area of the full circle, with the fraction determined by the ratio of the arc length (lateral surface) to the total circumference of the circle.
In the example given, how do you calculate the volume of a cone with radius 5 and height 12?
-The volume is calculated using the formula 1/3 * π * r² * h. Substituting r = 5 and h = 12, the volume is 314 cm³.
How would you calculate the surface area of a cone with a radius of 5 cm, height of 12 cm, and a slant height of 13 cm?
-To calculate the surface area, first calculate the area of the base: π * r² = π * 5² = 78.5 cm². Then, calculate the lateral surface area: π * r * s = π * 5 * 13 = 204.5 cm². The total surface area is the sum of both, which is 78.5 + 204.5 = 283 cm².
Outlines

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードMindmap

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードKeywords

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードHighlights

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードTranscripts

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレード関連動画をさらに表示

3 LUAS PERMUKAAN KERUCUT - BANGUN RUANG SISI LENGKUNG - KELAS 9 SMP

Pembuktian Luas Permukaan dan Volume Bangun Ruang Sisi Lengkung

Bangun Ruang | Matematika SD

Bangun Ruang Sisi Datar [Part 2] - Balok

Luas Permukaan Prisma dan Tabung Hal 213-215 Bab 6 Kelas 7 Kurikulum Merdeka
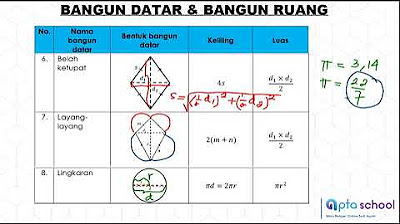
MATERI BANGUN DATAR DAN RUANG
5.0 / 5 (0 votes)
