Force of Impact Equation Derivation

Summary

In this educational video, the host and students explore Newton's Second Law and its relationship to momentum. Through a playful, interactive lesson during Spirit Week, they derive the Force of Impact Equation. The class discusses concepts like vectors, acceleration, momentum, and how they relate to collisions. They break down problems into multiple phases—free fall, collision, and post-collision. The lesson also introduces the concept of change in momentum, allowing the calculation of impact forces during collisions. The video provides both a fun and insightful look into physics, offering practical applications of Newton’s laws and momentum.

Takeaways

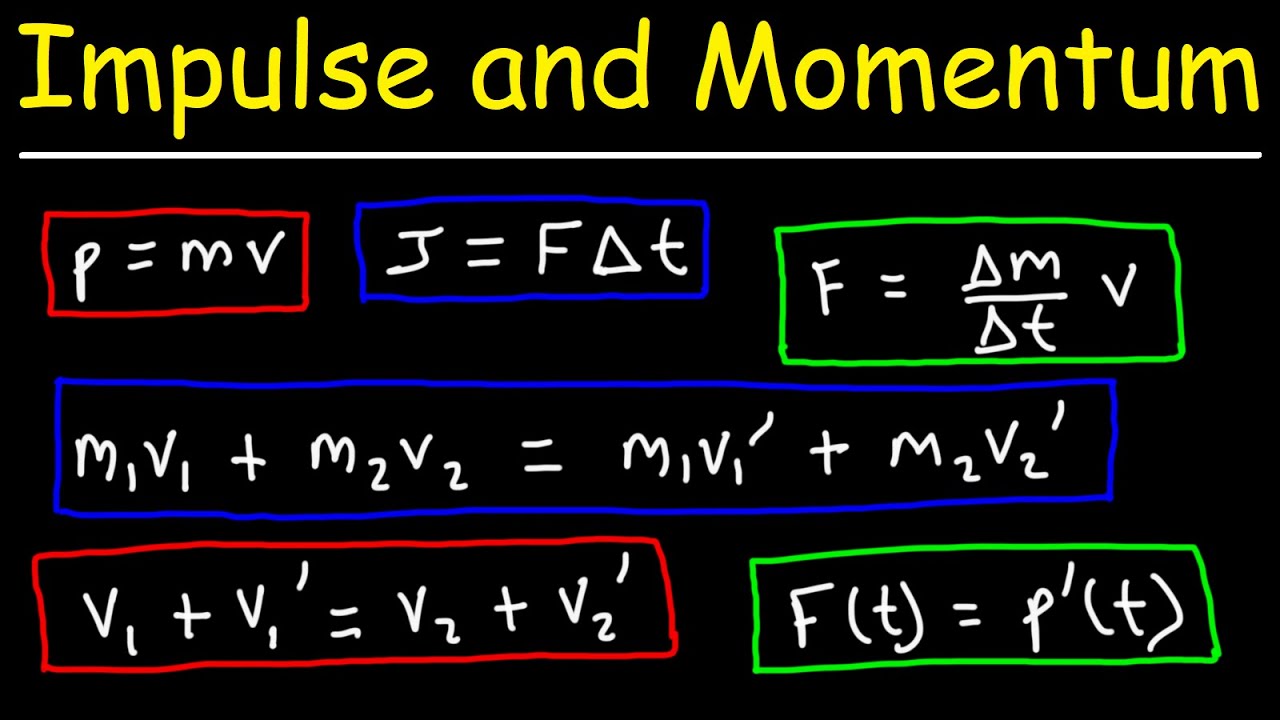
• 😀 Newton's Second Law is expressed as net force equals mass times acceleration (F = ma), where both force and acceleration are vectors.
• 😀 Acceleration is the change in velocity over the change in time, and it is important to understand that it is the 'change' in velocity.
• 😀 In the context of momentum, the equation for acceleration becomes Δv / Δt, where Δv is the change in velocity, and Δt is the change in time.
• 😀 The force equation can be rewritten in terms of momentum: net force = (mass × final velocity) - (mass × initial velocity) / Δt.
• 😀 Momentum is defined as the product of mass and velocity (p = mv). Changes in momentum are expressed as Δp = m × v_final - m × v_initial.
• 😀 Using momentum, the force during a collision is calculated as the rate of change of momentum with respect to time: net force = Δp / Δt.
• 😀 The net force equation in terms of momentum is crucial in analyzing collisions and impact forces, making it a key concept in physics.
• 😀 In more advanced physics, like AP Physics C, the equation for net force can be expressed as the derivative of momentum with respect to time (d/dt(p)).
• 😀 The Force of Impact during a collision can be analyzed in three phases: free fall before impact, the collision itself, and free fall after impact.
• 😀 Understanding force in terms of momentum allows for a more detailed and practical approach to problems like collisions, where time and velocity changes are important.
• 😀 The teaching environment is casual and engaging, with humor and participation from students, such as discussions about pajama day, making learning enjoyable and relatable.

Q & A

What is Newton's Second Law as described in the transcript?

Newton's Second Law states that the net force acting on an object equals its mass multiplied by its acceleration (F = ma). Both force and acceleration are vectors, meaning they have both magnitude and direction.

What is the equation for acceleration, as explained in the lesson?

The equation for acceleration is the change in velocity divided by the change in time (a = Δv / Δt), where Δv is the change in velocity and Δt is the change in time.

What is the significance of vectors in the context of force and acceleration?

Vectors are important because both force and acceleration have direction in addition to magnitude. The vector nature of these quantities means that both the size and direction of the force and acceleration need to be considered in calculations.

How is the force of impact during a collision derived in this script?

The force of impact is derived by analyzing the change in momentum during the collision. The equation used is net force = (Δmomentum) / (Δtime), where momentum is defined as mass times velocity, and both force and momentum are vectors.

What does 'change in velocity' equal in the context of this lesson?

'Change in velocity' (Δv) is defined as the final velocity (v_final) minus the initial velocity (v_initial). This is used to calculate acceleration and, ultimately, the force during a collision.

What is the relationship between momentum and velocity in this script?

Momentum is defined as mass times velocity (p = mv). The script differentiates between initial and final momentum, stating that momentum final equals mass times final velocity, and momentum initial equals mass times initial velocity.

What is the main shift in physics understanding highlighted in the lesson?

The shift is that, prior to this, students could only analyze objects before collisions. Now, with the new equation, they can analyze forces during collisions, which involves considering momentum and the change in momentum over time.

Why is the force of impact divided into three parts when analyzing a collision?

The collision is divided into three parts: (1) when the object is in free fall and moving downward, (2) when it collides with the ground, and (3) when the object is moving upward again. This breakdown helps to isolate different stages of the event for better analysis.

What does 'change in momentum' represent, and how is it used?

'Change in momentum' represents the difference between the final and initial momentum of an object. It is used to calculate the force acting on the object during the collision, as force equals the change in momentum divided by time.

Why does the teacher mention the importance of Calculus-based Physics courses?

The teacher mentions that Calculus-based Physics courses, like AP Physics C, would allow students to work with a more advanced form of the equation, specifically the derivative of momentum with respect to time, which provides a deeper understanding of forces during collisions.