Funkcje w 6 minut
Summary
TLDR本视频内容深入探讨了函数的基本概念及其应用,尤其是线性函数的表现。讲解了函数如何通过给定的输入值(如x)计算输出值(如y),并通过图形化表示帮助理解函数的运作。讨论了函数的定义、领域、值域及如何通过表格和图表来表示这些关系。还涉及了如何通过具体例子来计算函数的输出值,以及如何在图表中标注这些点。此外,讲解还提到了函数的不同类型,如线性函数,以及它们在数学中的应用,特别是在高中数学中备考的重要性。
Takeaways
- 😀 函数的定义是将一个集合的元素映射到另一个集合的元素。
- 😀 每个输入(自变量)对应唯一的输出(因变量),这就是函数的核心特性。
- 😀 函数的图形中,输入值(x)通过箭头指向输出值(y),箭头代表映射关系。
- 😀 图形中,x轴代表自变量,y轴代表因变量,函数图形帮助我们理解函数的变化。
- 😀 函数可以通过代数公式表示,例如 -2x + 3,这种公式可以用来计算不同x值对应的y值。
- 😀 给定函数的某个x值,可以计算出对应的y值,这一过程类似于向‘黑箱’输入一个值并得到输出。
- 😀 示例中的函数 -2x + 3 表明,当x为-3时,y的值为9,这个关系可以通过计算来验证。
- 😀 函数图形的解释包括如何根据x和y的坐标确定图形上的点,进一步理解函数的走势。
- 😀 对于任意输入x值,可以通过计算得到对应的输出y值,不限于整数输入,也可以是小数。
- 😀 不同类型的函数有不同的图形特征,比如线性函数、抛物线、正弦曲线等,学习这些特征有助于理解函数的性质。
Q & A
什么是函数?
-函数是一种数学关系,它将一个输入(称为自变量或定义域中的元素)映射到一个唯一的输出(称为值域中的元素)。换句话说,函数是从一个集合到另一个集合的映射,其中每个输入值都有一个对应的输出值。
在函数中,'x' 代表什么?
-'x' 代表函数的输入值,即定义域中的元素。它是函数的自变量,决定了函数输出的结果。
什么是函数的定义域?
-函数的定义域是所有可以作为输入的值的集合。它包括函数能够接受并映射到某些输出的所有可能的 'x' 值。
什么是函数的值域?
-函数的值域是函数可能输出的所有值的集合。这些值是函数在给定定义域内的所有可能输出。
如何通过计算得到函数的输出?
-要计算函数的输出,需要将特定的 'x' 值代入函数表达式中,然后根据函数规则进行计算。例如,对于函数 f(x) = -2x + 3,当 x = -3 时,输出是 f(-3) = -2(-3) + 3 = 9。
为什么函数的输出总是唯一的?
-根据函数的定义,每个输入值(即每个 'x')只能有一个对应的输出值。如果一个输入值对应多个输出值,那么它就不符合函数的定义。
函数如何在图形上表示?
-函数可以通过在坐标平面上绘制点来表示,其中 'x' 值对应水平轴,'y' 值对应垂直轴。每个点 (x, y) 表示函数在该点的值。函数图像的形状取决于函数类型,例如线性函数表现为直线,二次函数表现为抛物线等。
什么是线性函数?
-线性函数是函数的一种形式,其图像为一条直线,通常表示为 f(x) = ax + b 的形式,其中 a 和 b 是常数。线性函数的变化是匀速的,即每增加一个单位的 x,y 的变化是恒定的。
如何根据表格计算函数值?
-通过选择若干个 'x' 值并将它们代入函数表达式中,计算对应的 'y' 值。然后可以将这些 (x, y) 点绘制在坐标平面上,进而获得函数图像。
函数的图形如何帮助理解函数的行为?
-通过绘制函数的图形,可以直观地看到函数值如何随着自变量 'x' 的变化而变化。图形能够揭示函数的趋势,例如是否是递增的、递减的,或者是否有最大值或最小值。
Outlines

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードMindmap

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードKeywords

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードHighlights

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードTranscripts

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレード関連動画をさらに表示

Intro to the Laplace Transform & Three Examples

What does the second derivative actually do in math and physics?

What Is Entity Relationship Diagram ( ERD ) | ER Model Explained In DBMS With Examples

2funcvis

Teorema fundamental del cálculo: definición y ejemplos

0625 Distribución geométrica
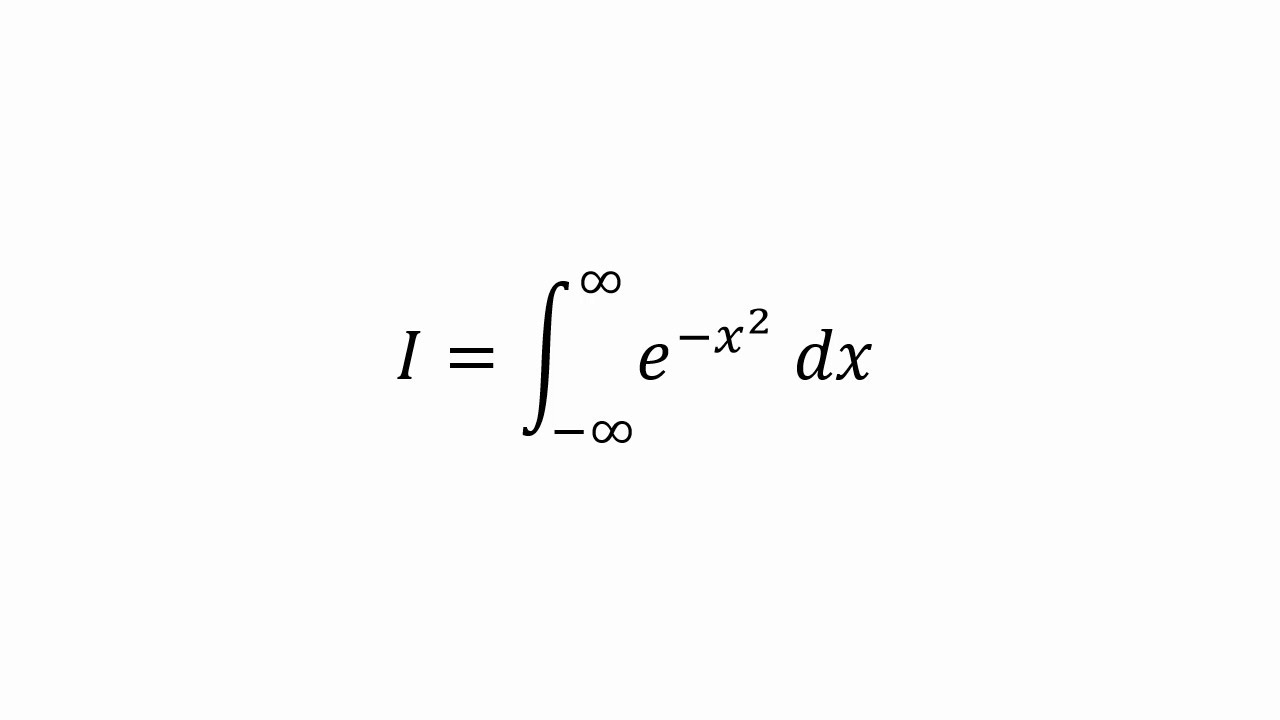
The Gaussian Integral
5.0 / 5 (0 votes)
