FUNÇÃO DO 2º GRAU: DEFINIÇÃO E GRÁFICO

Summary

This video introduces quadratic functions, also known as second-degree functions, focusing on their definition, structure, and graphical representation. It explains the standard form of quadratic functions (ax² + bx + c) and how to determine key components such as roots, vertex, and graph concavity. The presenter illustrates solving quadratic equations, finding the roots, and plotting the graph with practical examples. Additionally, it covers how the graph can either open upwards or downwards depending on the sign of 'a', with step-by-step guidance on calculating the vertex coordinates and determining the function's behavior.

Takeaways

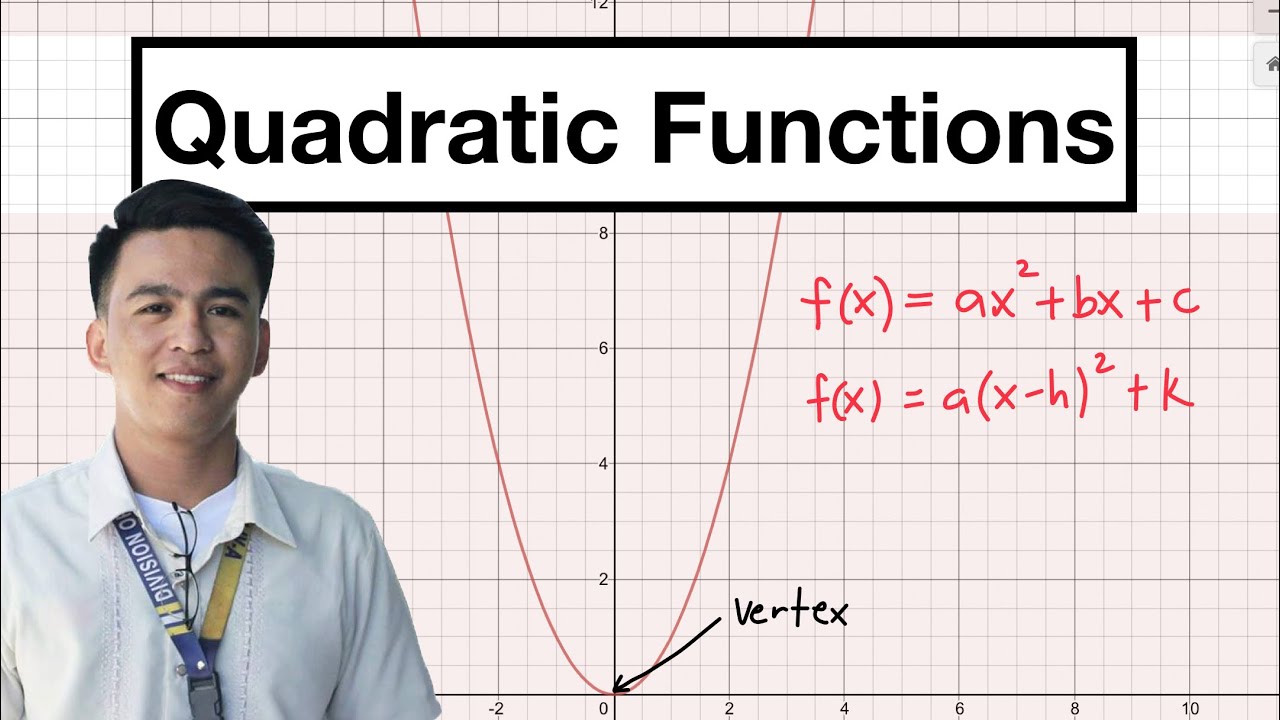
• 😀 Quadratic functions are expressed in the form f(x) = ax² + bx + c, where 'a' cannot be zero.
• 😀 To solve a quadratic function, you need to find its roots by solving the equation f(x) = 0.
• 😀 The roots (or x-intercepts) of a quadratic function can be found using the quadratic formula: x = (-b ± √(b² - 4ac)) / 2a.
• 😀 The graph of a quadratic function is a parabola, and it can either open upwards or downwards depending on the value of 'a'.
• 😀 If 'a' is positive, the parabola opens upwards, and if 'a' is negative, it opens downwards.
• 😀 The vertex of a quadratic function is the highest or lowest point on the graph, depending on the direction of the parabola.
• 😀 The x-coordinate of the vertex can be found using the formula x_v = -b / 2a.
• 😀 The y-coordinate of the vertex can be calculated using y_v = -Δ / 4a, where Δ = b² - 4ac.
• 😀 The y-intercept of the graph is the value of 'c', as it represents where the graph crosses the y-axis.
• 😀 When graphing a quadratic function, plot the roots, the vertex, and the y-intercept to sketch the graph accurately.

Q & A

What is the main topic of the video script?

The main topic of the video is quadratic functions, specifically their equations, graphs, and how to calculate the roots, vertex, and plot the graph.

What is a quadratic function, as explained in the video?

A quadratic function is a function of the form f(x) = ax² + bx + c, where a, b, and c are real numbers and a is not equal to zero. It represents a parabola when graphed.

What is the significance of the value 'a' in a quadratic function's graph?

The value of 'a' determines the direction of the parabola. If 'a' is positive, the parabola opens upwards (concave up), and if 'a' is negative, it opens downwards (concave down).

How do you calculate the roots of a quadratic function?

To calculate the roots of a quadratic function, set the function equal to zero (f(x) = 0) and solve for x. This can be done using factoring, completing the square, or the quadratic formula.

What is the vertex of a quadratic function, and how is it found?

The vertex is the point on the graph where the parabola changes direction. It can be found using the formula x = -b / 2a for the x-coordinate and then substituting this value into the function to find the y-coordinate.

How do the roots of the quadratic function relate to its graph?

The roots of the quadratic function are the points where the graph intersects the x-axis. These are the values of x where f(x) = 0.

What does the term 'delta' refer to in the context of solving quadratic equations?

Delta (Δ) refers to the discriminant in the quadratic formula, given by Δ = b² - 4ac. It helps determine the nature of the roots: if Δ > 0, there are two real roots; if Δ = 0, there is one real root; and if Δ < 0, there are no real roots.

What is the significance of the intersection with the y-axis in a quadratic function?

The intersection with the y-axis occurs where x = 0. The value of f(0) is equal to the constant term 'c' in the quadratic equation, and this gives the y-coordinate of the y-intercept.

What is the relationship between the sum and product of the roots in a quadratic function?

The sum of the roots is equal to -b/a, and the product of the roots is equal to c/a, based on Vieta's formulas.

How is the graph of a quadratic function drawn after finding the roots and vertex?

To draw the graph, plot the roots on the x-axis, the vertex on the graph, and the y-intercept on the y-axis. Then, sketch the parabola, ensuring the correct concavity based on the value of 'a'.