PROPERTIES OF LAPLACE TRANSFORM
Summary
TLDRThis comprehensive video script covers essential properties of Laplace transforms, including linearity, time shifting, time scaling, and derivatives in both time and Laplace domains. It provides in-depth proofs and step-by-step explanations, with a focus on the mathematical rigor behind each property. The video also introduces advanced concepts such as convolution and inverse Laplace transforms. Ideal for students and professionals, it serves as a thorough guide to understanding and applying these fundamental properties in Laplace transforms and their implications in mathematical analysis.
Takeaways
- 😀 The script discusses the Laplace Transform, a mathematical tool used for transforming functions from the time domain to the frequency domain.
- 😀 One of the key properties of the Laplace Transform covered is Linearity, which states that the transform of a sum is the sum of the transforms.
- 😀 The proof of the Linearity property involves integrating both terms separately, where constants can be taken outside the integral.
- 😀 Time-shifting property: If a function is shifted by a constant in time, its Laplace transform will change accordingly by multiplying it with an exponential term.
- 😀 The script details the process of proving time-shifting using the definition of Laplace Transform and step-by-step substitutions in the formula.
- 😀 Scaling property: When a function is multiplied by a constant in time, its Laplace transform is scaled by a reciprocal of that constant.
- 😀 The proof for scaling involves substituting the scaled time function into the Laplace formula and simplifying.
- 😀 The Time-Scaling property is important because it allows the transformation of functions that have been stretched or compressed in time.
- 😀 The Derivative Property states that the Laplace transform of the derivative of a function is related to the Laplace transform of the original function, involving multiplication by 's'.
- 😀 Convolution in the time domain becomes multiplication in the Laplace domain, and the script emphasizes the importance of understanding this property.
- 😀 The script also highlights the significance of knowing these Laplace Transform properties for solving differential equations and analyzing dynamic systems.
Q & A
What is the Linearity Property of Laplace Transform?
-The Linearity Property of Laplace Transform states that the Laplace Transform of a linear combination of signals is equal to the same linear combination of their individual Laplace Transforms. Mathematically, if L{f(t)} = F(s) and L{g(t)} = G(s), then L{a1 * f(t) + a2 * g(t)} = a1 * F(s) + a2 * G(s), where a1 and a2 are constants.
How do we prove the Linearity Property of Laplace Transform?
-To prove the Linearity Property, we start with the definition of the Laplace Transform for two signals, f(t) and g(t). The Laplace Transform is applied to the sum a1 * f(t) + a2 * g(t), and by applying the integral definition, the constants a1 and a2 can be taken outside the integral, proving the property.
What is the Time Shifting Property of the Laplace Transform?
-The Time Shifting Property of the Laplace Transform states that if a signal is shifted in time by t0, then the Laplace Transform of the shifted signal is given by L{f(t - t0)} = e^(-s * t0) * F(s). This means the time shift in the time domain corresponds to a multiplication by e^(-s * t0) in the s-domain.
How do we prove the Time Shifting Property?
-To prove the Time Shifting Property, we substitute the shifted function f(t - t0) into the definition of the Laplace Transform. After adjusting the limits of integration and making a substitution (t' = t - t0), we arrive at the result L{f(t - t0)} = e^(-s * t0) * F(s).
What does the Time Scaling Property of Laplace Transform refer to?
-The Time Scaling Property states that if a function is scaled by a constant factor 'a' in time, then its Laplace Transform is scaled by 1/a in the s-domain. Specifically, L{f(at)} = (1/a) * F(s/a), where 'a' is a constant scaling factor.
How is the Time Scaling Property of the Laplace Transform proven?
-The Time Scaling Property is proven by substituting the scaled function f(at) into the definition of the Laplace Transform. After a change of variables (t' = at), we can simplify the integral and obtain the result L{f(at)} = (1/a) * F(s/a).
What is the significance of the differentiation property in the Laplace Transform?
-The Differentiation Property of the Laplace Transform states that the Laplace Transform of the derivative of a function is related to the s-domain representation of the original function. Specifically, L{d/dt f(t)} = s * F(s) - f(0), where F(s) is the Laplace Transform of f(t).
How do you prove the Differentiation Property in Laplace Transforms?
-To prove the Differentiation Property, we start with the definition of the Laplace Transform and apply it to the derivative of f(t). The derivative term can be expressed as s * F(s) - f(0), where the f(0) term arises due to the evaluation of the original function at t=0.
What is the relationship between the Laplace Transform and its inverse?
-The Laplace Transform has an inverse that allows us to recover the original time-domain function from its s-domain representation. The inverse Laplace Transform is defined as L⁻¹{F(s)} = f(t), and is computed using various techniques such as partial fraction decomposition or the Bromwich integral.
How do you compute the Laplace Transform of a shifted or scaled function?
-To compute the Laplace Transform of a shifted or scaled function, we use the respective properties of the Laplace Transform. For time shifting, we apply the formula L{f(t - t0)} = e^(-s * t0) * F(s). For time scaling, we use the formula L{f(at)} = (1/a) * F(s/a). Both transformations involve modifying the original function in the time domain and applying the corresponding modifications in the s-domain.
Outlines

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードMindmap

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードKeywords

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードHighlights

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードTranscripts

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレード関連動画をさらに表示
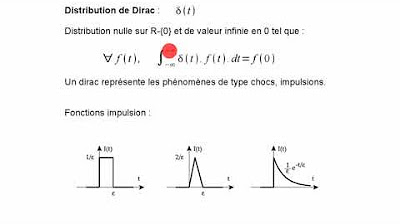
PCSI - video 2 - SLCI cours asservissements : outil Laplace

Fourier Transform Properties Explained

Review of Laplace Transform (Part 1)

PCSI - video 3 - SLCI cours asservissements - Partie2 : FT et schema blocs

Sistem Kendali 2.2. Transformasi Laplace

Lesson 1 - Laplace Transform Definition (Engineering Math)
5.0 / 5 (0 votes)
