O QUE SÃO FUNÇÕES MATEMÁTICAS? | QUER QUE DESENHE? | DESCOMPLICA
Summary
TLDRIn this educational video, the presenter explains key mathematical functions including affine, quadratic, exponential, logarithmic, and trigonometric functions. Each function is introduced with its formula, graphical representation, and key properties. The video emphasizes understanding the behavior of these functions based on their graphs and formulas, such as increasing or decreasing trends, roots, and the significance of discriminants. It also touches on the importance of analyzing the functions’ behavior in different mathematical contexts, offering an engaging and easy-to-understand approach for viewers to grasp essential mathematical concepts.
Takeaways
- 😀 Functions represent relationships between two sets and are defined by an expression and a graph.
- 😀 A linear function is of the form f(x) = ax + b, where a ≠ 0, and its graph is a straight line with a slope and intercept.
- 😀 The graph of a linear function can be increasing or decreasing depending on the slope: positive for increasing, negative for decreasing.
- 😀 A quadratic function is of the form f(x) = ax^2 + bx + c, with a ≠ 0. Its graph is a parabola that can open upwards or downwards.
- 😀 The vertex of a parabola is found at x = -b/(2a) and y = -Δ/(4a), where Δ = b² - 4ac is the discriminant.
- 😀 The discriminant (Δ) determines the number and nature of the roots of a quadratic function: two roots if Δ > 0, one root if Δ = 0, and no real roots if Δ < 0.
- 😀 Exponential functions are of the form f(x) = a^x, where a > 0 and a ≠ 1, and their graph can either represent growth (a > 1) or decay (0 < a < 1).
- 😀 Logarithmic functions are the inverse of exponential functions and are defined as f(x) = log_b(x), where b > 0 and b ≠ 1.
- 😀 The graph of a logarithmic function never touches the y-axis and intersects the x-axis at x = 1. Its behavior is increasing or decreasing depending on the base b.
- 😀 Trigonometric functions like sine (sin(x)) and cosine (cos(x)) are periodic and have specific patterns in different quadrants, where their values alternate between positive and negative.
Q & A
What is an affine function?
-An affine function is a linear function of the form f(x) = ax + b, where a and b are real numbers, and a is not equal to zero. Its graph is a straight line that intersects the y-axis at b. If a > 0, the function is increasing, and if a < 0, the function is decreasing.
How can you determine whether an affine function's graph is increasing or decreasing?
-If the coefficient 'a' of the affine function f(x) = ax + b is positive (a > 0), the graph will be increasing. If 'a' is negative (a < 0), the graph will be decreasing.
What does the graph of a quadratic function look like?
-The graph of a quadratic function, f(x) = ax^2 + bx + c, is a parabola. If the coefficient 'a' is positive, the parabola opens upwards and has a minimum point. If 'a' is negative, the parabola opens downwards and has a maximum point.
What is the significance of the discriminant in a quadratic function?
-The discriminant, denoted as Δ (Delta), determines the nature of the roots of a quadratic equation. If Δ > 0, the graph intersects the x-axis at two points. If Δ = 0, the graph is tangent to the x-axis, with one repeated root. If Δ < 0, the graph does not intersect the x-axis and has no real roots.
How do you find the vertex of a parabola for a quadratic function?
-The vertex of a parabola for the quadratic function f(x) = ax^2 + bx + c can be found using the formulas: x_v = -b / (2a) for the x-coordinate and y_v = -Δ / (4a) for the y-coordinate, where Δ is the discriminant.
What is an exponential function and its general form?
-An exponential function is a function where the variable is in the exponent. It has the form f(x) = a^x, where 'a' is a positive real number, and 'a' is not equal to 1. The graph of this function is a curve that grows rapidly if a > 1, and decays if 0 < a < 1.
What happens to the graph of an exponential function when a > 1?
-When a > 1 in the exponential function f(x) = a^x, the graph is increasing, meaning it rises steeply as x increases.
What is a logarithmic function, and how is it related to an exponential function?
-A logarithmic function is the inverse of an exponential function. It has the form f(x) = log_b(x), where 'b' is a positive real number, and b is not equal to 1. The graph of a logarithmic function is increasing if b > 1, and decreasing if 0 < b < 1.
What is the key feature of the graph of a logarithmic function?
-The graph of a logarithmic function never touches the y-axis and always cuts the x-axis at x = 1. It is always positive for x > 0, and its behavior depends on the base 'b'. If b > 1, the function is increasing; if 0 < b < 1, the function is decreasing.
What are trigonometric functions and how are they periodic?
-Trigonometric functions, such as sine and cosine, are periodic functions related to the unit circle. They repeat their values in regular intervals, known as the period. The sine and cosine functions have a period of 2π, meaning their graphs repeat every 2π units.
Outlines

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードMindmap

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードKeywords

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードHighlights

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードTranscripts

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレード関連動画をさらに表示
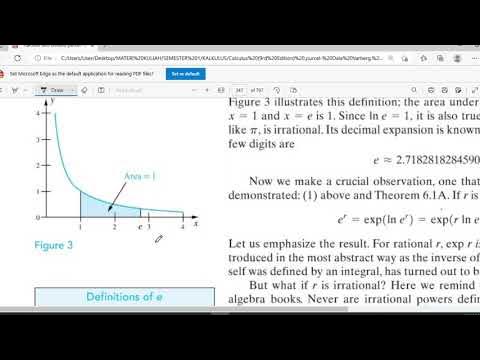
Fungsi Transenden 3 (Fungsi Eksponensial Natural)

Introduction to Exponential Functions - Nerdstudy

Logarithmic Functions | Transforming Logarithmic Equation to Exponential Form and Vice Versa

Lec 52 - Logarithmic Functions
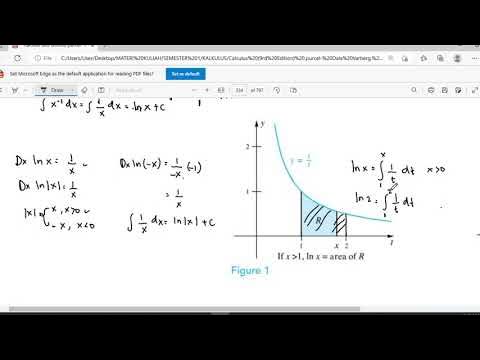
Fungsi Transenden 1 (Logaritma Natural/Ln)

Solving Logarithmic Inequalities | General Mathematics
5.0 / 5 (0 votes)
