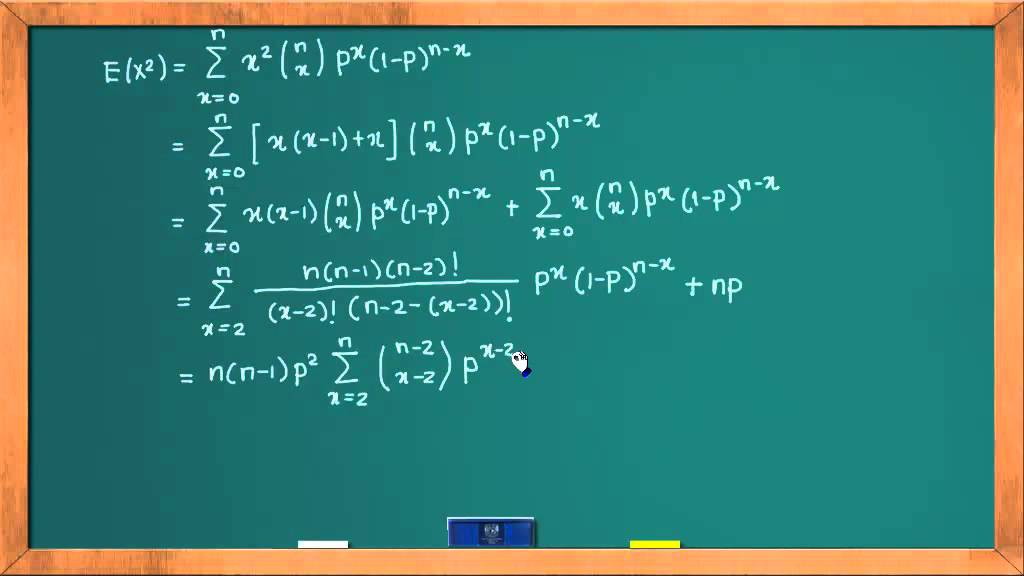0625 Distribución binomial negativa

Summary

This video introduces the Negative Binomial Distribution, which generalizes the Geometric Distribution by modeling the number of failures before achieving a fixed number of successes in a series of independent Bernoulli trials. The script explains the probability function, expectation, and variance of this distribution, highlighting how it simplifies to the Geometric Distribution when the number of successes is one. It concludes with a real-world example of a couple attempting to have three girls, illustrating how to use the Negative Binomial Distribution to calculate the expected number of children in total.

Takeaways

• 😀 The negative binomial distribution is a generalization of the geometric distribution, where the number of failures before a fixed number of successes is counted.
• 😀 It is based on a series of independent Bernoulli trials, each with a success probability of p, where the outcome is a series of successes and failures.
• 😀 The random variable X represents the number of failures before obtaining a specified number of successes (r), with possible values 0, 1, 2, 3, etc.
• 😀 The probability mass function (PMF) for a negative binomial distribution is expressed as a combination formula involving the number of failures and successes.
• 😀 The formula for the PMF is given by: P(X=x) = C(r+x-1, x) * p^r * (1-p)^x.
• 😀 The expectation (mean) of a negative binomial random variable X is given by E(X) = r * (1-p) / p.
• 😀 The variance of X in a negative binomial distribution is given by Var(X) = r * (1-p) / p^2.
• 😀 When the parameter r is equal to 1, the negative binomial distribution reduces to the geometric distribution.
• 😀 The negative binomial distribution does not have a compact form for the cumulative distribution function (CDF).
• 😀 An example of the negative binomial distribution is the problem of determining the average number of children a couple will have before they have three daughters, given that the probability of having a girl is 3/7.
• 😀 The expected total number of children for the couple in the example is calculated as E(X) + 3, where X is the number of boys before having three girls, resulting in an expected total of 7 children.

Q & A

What is the negative binomial distribution?

The negative binomial distribution is a generalization of the geometric distribution, where the number of failures is counted before obtaining a fixed number of successes in a series of independent Bernoulli trials.

How does the negative binomial distribution differ from the geometric distribution?

While the geometric distribution counts the number of failures before the first success, the negative binomial distribution counts the number of failures before obtaining a fixed number of successes.

What are the parameters of the negative binomial distribution?

The negative binomial distribution has two parameters: r (the number of successes) and p (the probability of success in each trial).

What is the probability mass function (PMF) for the negative binomial distribution?

The PMF is given by the formula: P(X = x) = C(r + x - 1, x) * p^r * (1 - p)^x, where C represents the binomial coefficient, r is the number of successes, p is the probability of success, and x is the number of failures.

How is the expected value (mean) of a negative binomial distribution calculated?

The expected value (mean) of a negative binomial distribution is calculated as E(X) = r * (1 - p) / p, where r is the number of successes and p is the probability of success in each trial.

What is the variance of a negative binomial distribution?

The variance of a negative binomial distribution is given by Var(X) = r * (1 - p) / p^2, where r is the number of successes and p is the probability of success.

What is the relationship between the negative binomial and geometric distributions?

When the parameter r equals 1, the negative binomial distribution becomes the geometric distribution, which models the number of failures before the first success.

How do we calculate the expected number of children for a family wanting a fixed number of daughters?

For a family wanting a fixed number of daughters, we use the negative binomial distribution to model the number of children born before the desired number of daughters. The expected total number of children is the expected number of failures (sons) plus the desired number of daughters.

What is the significance of the binomial coefficient in the negative binomial distribution formula?

The binomial coefficient in the negative binomial distribution formula accounts for the number of different ways in which the successes and failures can be arranged in the sequence of trials, ensuring that the last trial is a success and the previous trials include the required number of failures.

Can the negative binomial distribution be applied to real-life scenarios?

Yes, the negative binomial distribution is commonly applied in real-life scenarios where we need to model the number of failures before a fixed number of successes, such as in quality control, medical trials, or in the example of a family trying to have a fixed number of children of a particular gender.