Frequency response Part 1
Summary
TLDRThis video discusses the concept of frequency response in control systems, focusing on how a system's steady-state response behaves when subjected to a sinusoidal input. The speaker explains the process of analyzing systems with components such as resistors and capacitors, using Laplace transforms and simulations. Key concepts like amplitude, phase shift, and delay time are explored, demonstrating how to compute the magnitude and phase of a system’s response. The video also introduces the use of Bode plots for visualizing the system’s frequency response, providing a comprehensive explanation suitable for students and practitioners of control systems.
Takeaways
- 😀 Frequency response describes the steady-state behavior of a system when a sinusoidal input is applied.
- 😀 Sinusoidal inputs can be in the form of either sine or cosine waves, both classified as sinusoidal signals.
- 😀 In frequency response, the output signal maintains the same frequency as the input, but its amplitude and phase may change.
- 😀 The phase difference between input and output signals in systems like RC circuits is referred to as 'delay time'.
- 😀 The output amplitude is related to the input amplitude through the system's gain, represented as |G|.
- 😀 Phase shift (or delay time) is a critical factor in understanding how the output is delayed relative to the input signal.
- 😀 Laplace transforms are used to derive the time-domain output from the system's transfer function in the frequency domain.
- 😀 For a simple RC circuit, when a sinusoidal input is applied, the output signal can be calculated using the transfer function and Laplace inverse.
- 😀 The general formula for frequency response shows that the output of a linear system will have the same frequency as the input, but altered amplitude and phase.
- 😀 Bode plots are used to visualize the frequency response by plotting both gain and phase shift as functions of input frequency.
- 😀 The phase shift in frequency response increases with higher input frequencies, meaning higher frequencies introduce larger delays in the system.
Q & A
What is frequency response in the context of system control design?
-Frequency response refers to the steady-state response of a system when it is given a sinusoidal input. The input can be a sine or cosine wave, and the output's amplitude and phase may differ from the input's, depending on the system's characteristics.
What kind of input signal is used in frequency response analysis?
-The input signal used in frequency response analysis is a sinusoidal signal, which can be either a sine or cosine wave. These signals are used to analyze how the system responds to periodic inputs.
How does the frequency response of a system relate to its transfer function?
-The frequency response of a system is closely related to its transfer function, which is a mathematical representation of the system. The transfer function allows the calculation of how the system responds to sinusoidal inputs at different frequencies.
What does a Bode plot represent in frequency response analysis?
-A Bode plot represents the magnitude and phase of the frequency response of a system. It is typically used to visualize how a system’s gain and phase shift vary with frequency. A Bode plot consists of two plots: one for gain and one for phase.
What is the relationship between the input and output in a linear system when using sinusoidal signals?
-In a linear system, if the input is a sinusoidal signal, the output will also be sinusoidal, but with a different amplitude and phase. The frequency of the output will match the input, but the amplitude is scaled by the system's gain, and the phase is shifted.
How is the amplitude of the output determined in a sinusoidal steady-state system?
-The amplitude of the output in a steady-state sinusoidal system is determined by multiplying the amplitude of the input by the magnitude of the system’s transfer function, denoted as |G|.
What does a phase shift (delay time) in the output signal indicate?
-A phase shift (or delay time) indicates a time difference between when the input signal reaches a certain point and when the output signal reaches the corresponding point. This delay is represented as a phase shift in the frequency response, where the phase angle of the output differs from the phase angle of the input.
How can the delay time or phase shift be calculated from a frequency response?
-The delay time or phase shift can be calculated by measuring the phase difference between the input and output signals at a particular frequency. This phase difference can be determined by calculating the phase angle of the system’s transfer function and comparing it to the input signal.
What is the significance of the Laplace transform in analyzing the output of a system to a sinusoidal input?
-The Laplace transform is used to convert the input signal, typically a sinusoidal function, into the Laplace domain. By using the system’s transfer function in the Laplace domain, one can analytically determine the system’s response to sinusoidal inputs, including calculating the output in both the time and frequency domains.
What are the steps involved in analyzing a system’s frequency response using a transfer function?
-The steps involved in analyzing a system's frequency response include: 1) Express the system’s transfer function, 2) Replace the Laplace variable with the imaginary component jω (where ω is the frequency), 3) Calculate the magnitude and phase of the system at various frequencies, and 4) Use these values to construct a Bode plot or directly analyze the system’s output.
Outlines

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードMindmap

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードKeywords

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードHighlights

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードTranscripts

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレード関連動画をさらに表示

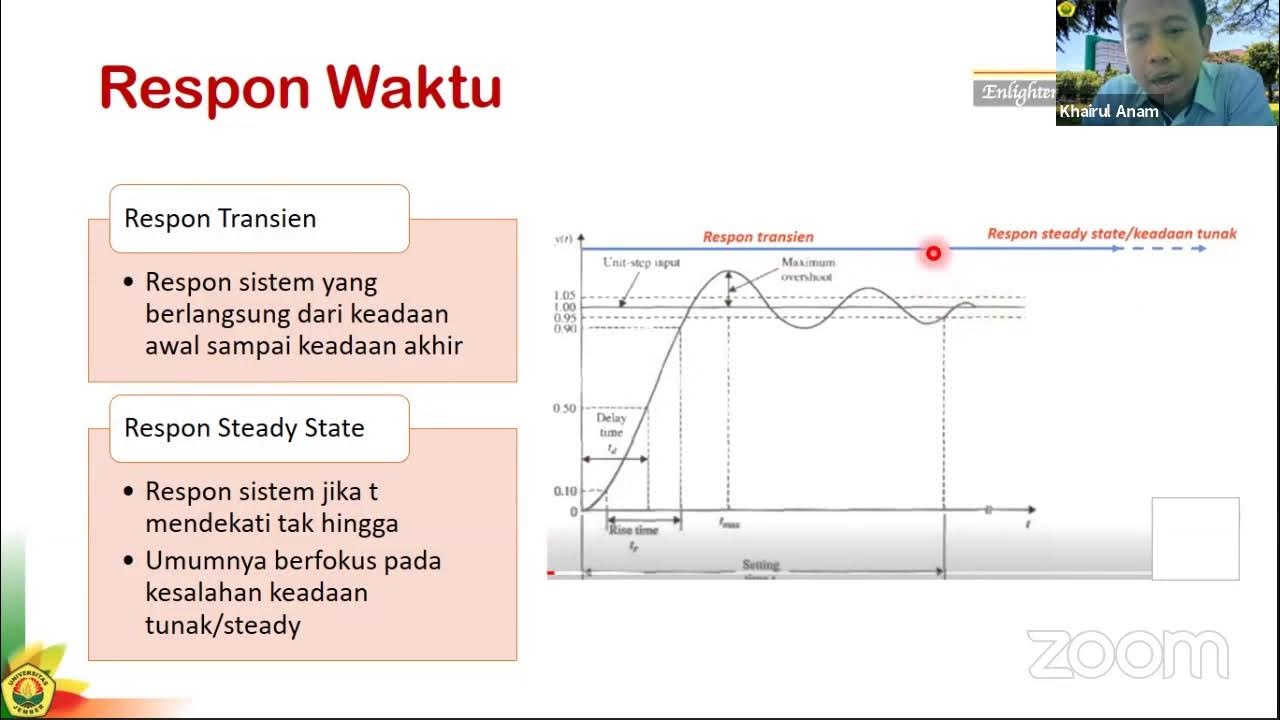
Illustration of sinusoidal transient and steady-state in time-response of LTI systems

System Response Characteristics
Sistem Kontrol #3a: Analisis Repon Sistem - Pendahuluan

#173 Time response of first order control system || EC Academy

Memahami Bode Plot (Seri Respon Frekuensi part1)

Control System Lectures - Bode Plots, Introduction
5.0 / 5 (0 votes)
