[SER222] M02_02 The Algorithm (6/8): Implementation
Summary
TLDREn este video se explica el algoritmo de ordenamiento Merge Sort, detallando su implementación paso a paso. Se aborda la creación de un arreglo auxiliar para facilitar la fusión de elementos ordenados, y cómo el algoritmo divide recursivamente el arreglo en mitades para ordenarlas. El punto clave es el proceso de fusión, donde se combinan los sub-arreglos ordenados en el arreglo original. Se destacan aspectos como la complejidad temporal de O(n log n) y la necesidad de memoria adicional debido al arreglo auxiliar. Merge Sort es eficiente y robusto, aunque presenta un costo de memoria.
Takeaways
- 😀 La función principal de Merge Sort utiliza un arreglo auxiliar para almacenar temporalmente los elementos durante la fusión.
- 😀 El algoritmo Merge Sort es un algoritmo de dividir y conquistar que divide el arreglo en subarreglos, los ordena recursivamente y luego los fusiona en orden.
- 😀 La complejidad temporal de Merge Sort es O(n log n), pero hay un costo de memoria adicional debido al arreglo auxiliar.
- 😀 El caso base del algoritmo ocurre cuando el subarreglo tiene uno o menos elementos, lo que significa que ya está ordenado.
- 😀 Se utiliza la fórmula 'lo + hi - lo / 2' para calcular el punto medio de un subarreglo, evitando posibles errores de desbordamiento de enteros.
- 😀 La condición de igualdad entre 'lo' y 'hi' indica que el subarreglo tiene un solo elemento, por lo que no se necesita más ordenamiento.
- 😀 El proceso de fusión asume que los subarreglos ya están ordenados, por lo que simplemente los combina en orden.
- 😀 El algoritmo recursivo se detiene cuando los índices 'lo' y 'hi' son iguales, indicando que solo queda un elemento para ordenar.
- 😀 La memoria adicional utilizada por Merge Sort no afecta su complejidad temporal, pero es una consideración importante en términos de uso de recursos.
- 😀 La función 'merge()' es el corazón del algoritmo, ya que realiza la comparación y la inserción de los elementos ordenados en el arreglo auxiliar.
Q & A
¿Qué es un arreglo auxiliar y por qué es necesario en el algoritmo de Merge Sort?
-El arreglo auxiliar es un espacio temporal utilizado para almacenar los elementos mientras se realiza la combinación o 'merge'. Es necesario porque permite que los subarreglos ordenados se fusionen de manera eficiente sin modificar el arreglo original hasta que se complete el proceso.
¿Cuáles son los cuatro parámetros que recibe la función principal 'sort' en Merge Sort?
-Los cuatro parámetros que recibe la función 'sort' son: el arreglo a ordenar ('a'), el arreglo auxiliar ('aux'), el índice de inicio del subarreglo a ordenar ('lo'), y el índice final del subarreglo ('hi').
¿Cómo se calcula el punto medio de un subarreglo en Merge Sort y por qué es importante?
-El punto medio se calcula con la fórmula 'lo + (hi - lo) / 2'. Esto es importante porque divide el arreglo en dos mitades de manera eficiente. Se utiliza esta fórmula para evitar un posible desbordamiento de enteros que podría ocurrir si se usara '(lo + hi) / 2'.
¿Cuál es el caso base del algoritmo de Merge Sort?
-El caso base ocurre cuando un subarreglo tiene uno o cero elementos. En este caso, no es necesario ordenar el subarreglo, ya que se considera que está ordenado por defecto.
¿Qué sucede si el índice 'lo' es mayor que 'hi' en el algoritmo de Merge Sort?
-Si 'lo' es mayor que 'hi', significa que hubo un error numérico durante el proceso de división y se ha llegado a un subarreglo vacío o con índices invertidos. Esto indica que no hay más elementos para ordenar y el algoritmo termina en ese punto.
¿Cómo maneja Merge Sort la fusión de dos subarreglos ordenados?
-Una vez que los subarreglos son ordenados recursivamente, la función 'merge' se encarga de fusionarlos en un solo subarreglo ordenado. Toma los índices 'lo', 'mid' y 'hi' para saber cómo dividir y combinar ambos subarreglos.
¿Cuál es la complejidad temporal de Merge Sort y qué implica esto?
-La complejidad temporal de Merge Sort es O(n log n), lo que significa que el tiempo de ejecución crece proporcionalmente al tamaño del arreglo multiplicado por el logaritmo de su tamaño. Es eficiente incluso con arreglos grandes.
¿Qué significa que Merge Sort sea un algoritmo estable?
-Que Merge Sort sea estable significa que si hay elementos iguales en el arreglo, el algoritmo mantendrá su orden relativo original después de la ordenación, lo cual es importante en ciertos casos, como cuando se desea preservar la estabilidad de los datos.
¿Qué problemas podría ocasionar la fórmula '(lo + hi) / 2' al calcular el punto medio?
-La fórmula '(lo + hi) / 2' puede ocasionar un desbordamiento de enteros si 'lo' y 'hi' son números muy grandes, lo cual puede llevar a errores en la ejecución del programa. Es por eso que se usa 'lo + (hi - lo) / 2' para evitar este problema.
¿Por qué es importante el uso de recursión en el algoritmo de Merge Sort?
-La recursión en Merge Sort permite dividir el arreglo en subarreglos más pequeños, lo que facilita el proceso de ordenación. Cada subarreglo se ordena de manera independiente y luego se fusionan de nuevo en un arreglo completamente ordenado.
Outlines

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードMindmap

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードKeywords

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードHighlights

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードTranscripts

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレード関連動画をさらに表示
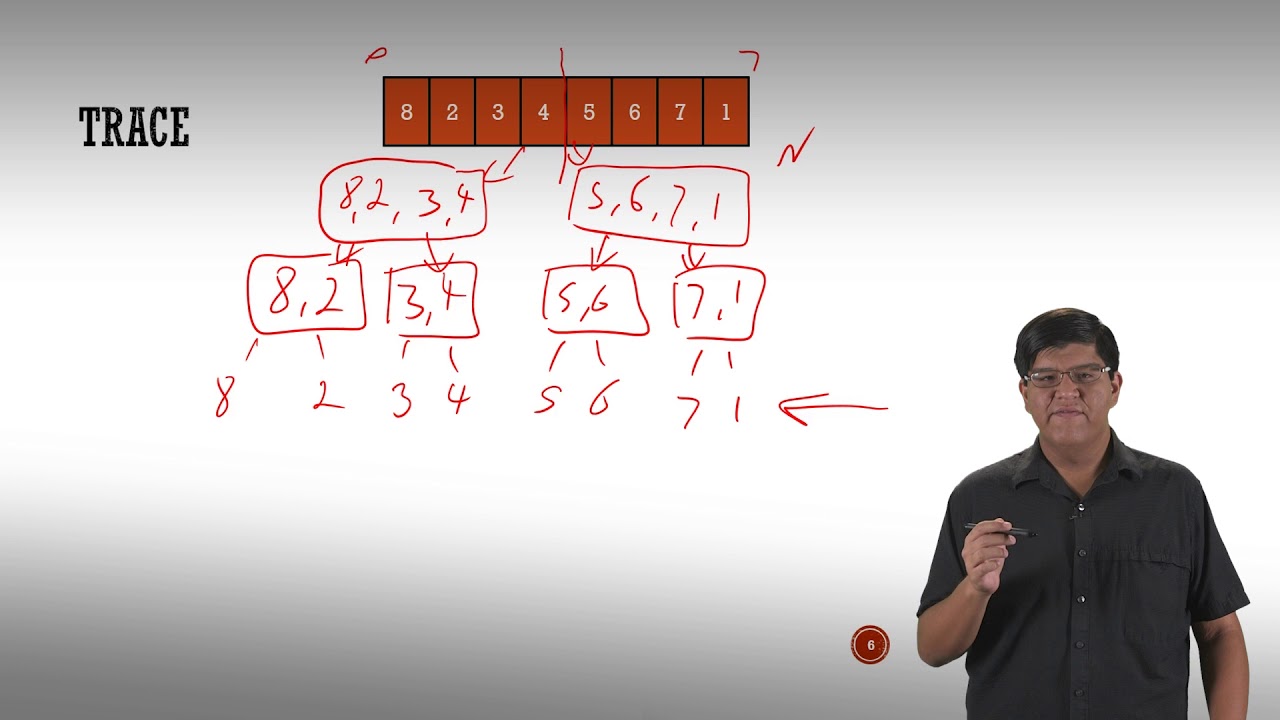
[SER222] M02_02 The Algorithm (4/8): Algorithm Trace

[SER222] M02_02 The Algorithm (5/8): Visual Trace

[SER222] M02_02 The Algorithm (7/8): Implementing Merge

[SER222] M02_01 Shellsort (2/5): Conceptual Trace

52. Programación en C++ || Ordenamientos || Ordenamiento por Selección

Ordenamiento Quicksort (Rápido!) en Java
5.0 / 5 (0 votes)
