APLICACIÓN DE LA DERIVADA AL TRAZADO DE CURVAS - Ejercicio 2
Summary
TLDRThis video explains how to analyze and graph a cubic polynomial function using derivatives. It covers key steps like determining the domain, calculating the first and second derivatives, finding critical points, and analyzing intervals of increase and decrease. The script walks through methods for identifying maximum and minimum points, determining concavity, and constructing the graph based on calculated values. The explanation is thorough, guiding viewers through the process of obtaining critical information such as inflection points and function behavior. The final output is a well-constructed graph with clear insights into the function's characteristics.
Takeaways
- 😀 The domain of a cubic polynomial function is all real numbers (R), meaning x can take any value.
- 😀 The first derivative of the function is calculated as F'(x) = 3x² - 12x - 15, representing the rate of change of the function.
- 😀 The second derivative is F''(x) = 6x - 12, which helps determine concavity and points of inflection.
- 😀 Critical points are found by setting the first derivative equal to zero, resulting in x = -1 and x = 5 as the critical points of the function.
- 😀 The function is increasing in intervals where the first derivative is positive and decreasing where the first derivative is negative.
- 😀 The first derivative test reveals that x = -1 is a local maximum and x = 5 is a local minimum for the function.
- 😀 Points of inflection, where the function changes concavity, occur where the second derivative is zero, which happens at x = 2.
- 😀 The function is concave down (F''(x) < 0) on the interval (-∞, 2) and concave up (F''(x) > 0) on the interval (2, ∞).
- 😀 The key points on the graph include the critical points (-1, 48) and (5, -60), and the inflection point (2, -6).
- 😀 The function intersects the y-axis at (0, 40), and the x-axis at approximately (-3.1, 0), (1.8, 0), and (7.3, 0).
Q & A
What is the domain of the cubic function discussed in the script?
-The domain of the cubic function is the set of all real numbers, as it is a polynomial function of degree 3, and polynomials are defined for all real values of x.
How do we calculate the first derivative of the cubic function?
-To calculate the first derivative of the cubic function, we differentiate each term of the polynomial. For example, the derivative of x^3 is 3x^2, and for terms like 6x^2, the derivative is 12x.
What is the importance of the second derivative in analyzing the function?
-The second derivative helps determine the concavity of the function and also aids in finding points of inflection, where the function changes from being concave up to concave down or vice versa.
How do we find the critical points of the function?
-Critical points are found by setting the first derivative equal to zero and solving the resulting equation. These points correspond to where the slope of the tangent is horizontal, indicating local maxima, minima, or inflection points.
What method is used to solve the equation for critical points, and what are the solutions?
-The equation for critical points is solved by factoring. The factored equation 3(x - 5)(x + 1) = 0 gives the solutions x = -1 and x = 5, which are the x-values of the critical points.
What does the sign of the first derivative tell us about the function?
-The sign of the first derivative determines whether the function is increasing or decreasing. If the first derivative is positive in an interval, the function is increasing; if it is negative, the function is decreasing.
How are the intervals of increase and decrease determined for the function?
-Intervals of increase and decrease are determined by analyzing the sign of the first derivative over different intervals. For each interval, a test value is selected and substituted into the first derivative to check whether the derivative is positive or negative.
What do we conclude about the nature of the critical points based on the first derivative test?
-From the first derivative test, we conclude that at x = -1, the function has a local maximum, and at x = 5, the function has a local minimum. This is because the function changes from increasing to decreasing at x = -1 and from decreasing to increasing at x = 5.
How do we find the point of inflection of the function?
-The point of inflection is found by setting the second derivative equal to zero and solving for x. In this case, solving 6x - 12 = 0 gives x = 2 as the point of inflection.
What is the significance of the second derivative test in determining concavity?
-The second derivative test helps identify the concavity of the function. If the second derivative is positive on an interval, the function is concave up; if it is negative, the function is concave down.
Outlines

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードMindmap

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードKeywords

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードHighlights

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードTranscripts

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレード関連動画をさらに表示

Derivada de una función polinomial (paso a paso) 👌👆. Cálculo diferencial. 2

Higher Order Derivatives

X- AND Y- INTERCEPTS OF GRAPHS OF POLYNOMIAL FUNCTION|| GRADE 10 MATHEMATICS Q2
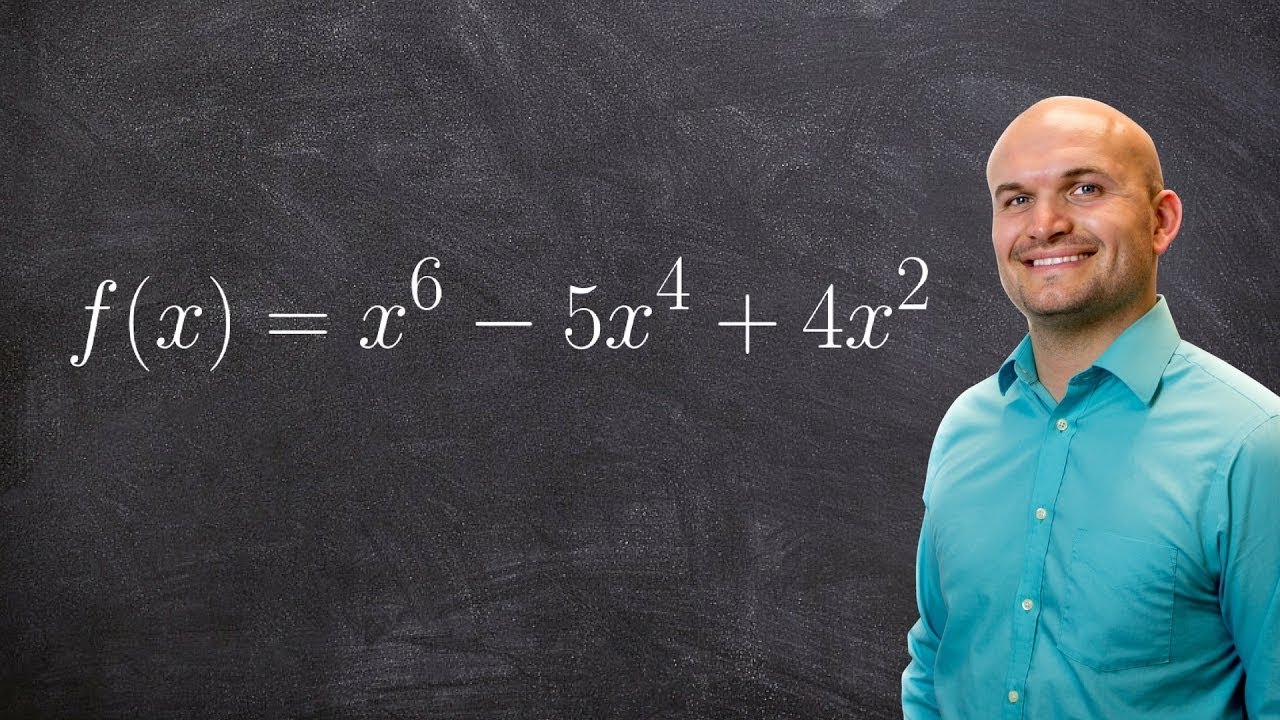
How do we find multiplicity and use it to graph a polynomial

Fundamental Theorem of Algebra

Grade 10 - Illustrating and graphing polynomial functions | SirABC
5.0 / 5 (0 votes)
