Kalkulus 2 Pertemuan 9 Aisyah Fy Part 5

Summary

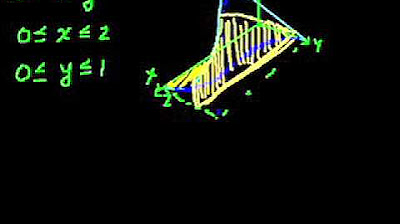
The transcript discusses calculating the volume of a solid bounded by the equations x² + y² = 4 and y + z = 4, with z = 0. It explains the importance of sketching the solid to understand the volume calculation process. The solid's base is a circle with a radius of 2, and the area is analyzed using integration techniques. The speaker highlights the use of trigonometric substitution for integration, ultimately leading to a result of 16π for the volume. The explanation emphasizes the step-by-step approach in applying integration to solve for the solid's volume.

Takeaways

• 😀 The volume of a solid bounded by specific equations can be calculated using integration techniques.
• 📝 The solid is defined by the equations: x² + y² = 4, y + z = 4, and z = 0.
• 📏 A sketch of the solid is essential to visualize the region for volume calculation.
• 🔍 The equation x² + y² = 4 represents a circle with a radius of 2 in the xy-plane.
• 📈 The line y + z = 4 intersects the z-axis at z = 4, forming a slanted plane.
• ⚖️ The volume is calculated only above the xy-plane (z = 0).
• 🧮 To find the volume, integration must be set up carefully with the correct bounds.
• 🔄 The integration approach involves changing the order of integration based on the shape of the region.
• 📊 The integral is evaluated with respect to y first, then x, using proper substitutions.
• 🎉 The final result of the volume calculation is found to be 16π.

Q & A

What is the solid defined by in the given transcript?

The solid is defined by the equations x² + y² = 4, y + z = 4, and z = 0.

What geometric shape is formed by the equation x² + y² = 4?

This equation describes a circle with a radius of 2 in the x-y plane.

What role does the equation y + z = 4 play in defining the solid?

This equation defines a slanted plane that intersects the z-axis at z = 4.

Why is z = 0 included in the equations?

The equation z = 0 represents the x-y plane, which acts as the lower boundary of the solid.

What is the first step in calculating the volume of the solid?

The first step is to visualize the solid and identify its boundaries based on the given equations.

How can the volume be expressed as an integral?

The volume can be expressed as a double integral over the region defined by the circle in the x-y plane.

What are the limits for the y integration based on the circle's equation?

The limits for y are from -√(4 - x²) to √(4 - x²).

What does the inner integral represent in the volume calculation?

The inner integral computes the height (z) of the solid at each point (x, y) based on the equation z = 4 - y.

What is the result of the volume integral after evaluation?

The result of the volume integral is V = 16π.

What integration technique might be useful in solving the integrals involved?

Trigonometric substitution may be useful, especially when dealing with integrals involving square roots.