Derivada de un cociente | Ejemplo 2 | Reglas de derivación
Summary
TLDREn este video, se explica cómo calcular la derivada de una función que es un cociente, utilizando una fórmula simplificada. El presentador muestra paso a paso el proceso de derivación, comenzando con la derivada de la parte superior e inferior del cociente y aplicando la regla del cociente. Se realizan multiplicaciones de binomios y se explican conceptos clave, como la importancia de mantener el signo negativo en las operaciones. Al final, se deja un ejercicio para que los espectadores practiquen lo aprendido, invitándolos a suscribirse y participar en el canal.
Takeaways
- 😀 En este video se explica cómo hallar la derivada de un cociente de funciones, subiendo el nivel de dificultad.
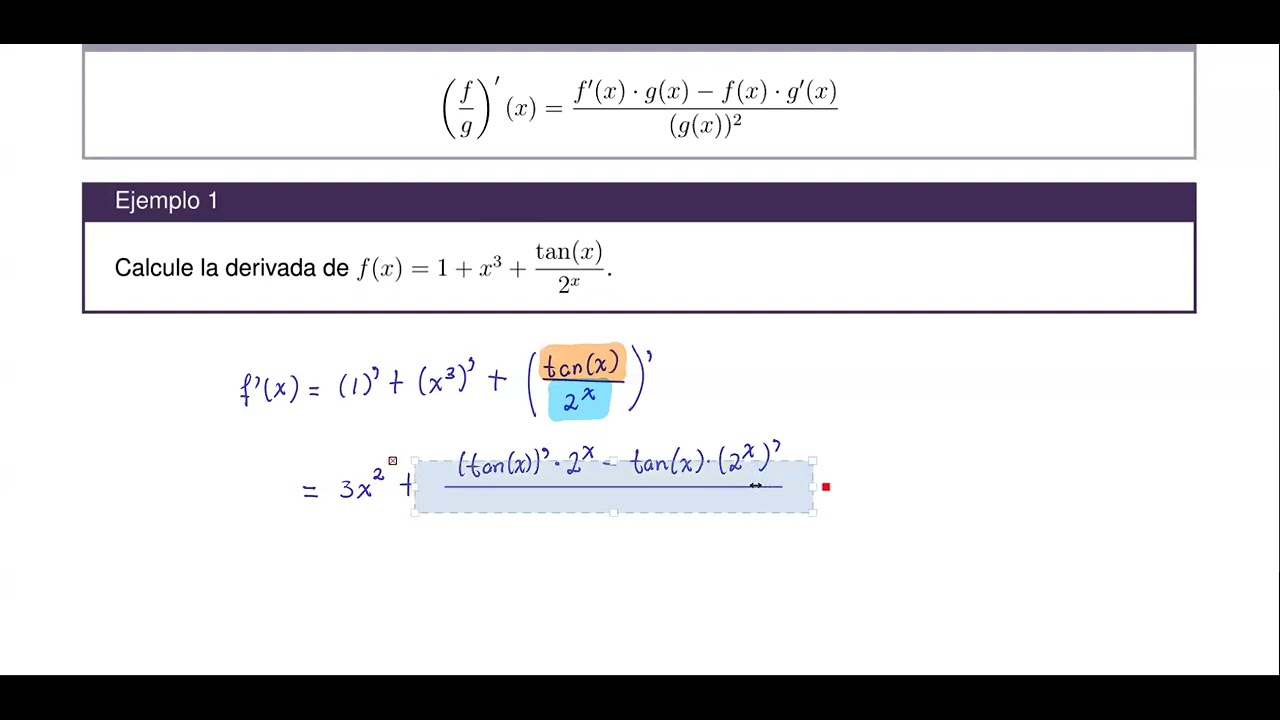
- 📖 Se introduce la fórmula para calcular la derivada de un cociente: (f/g)' = (g*f' - f*g') / g².
- 📝 La derivada del numerador se obtiene aplicando la regla de derivación estándar a cada término de la función.
- 🔄 Se enfatiza la importancia de aplicar correctamente la derivada a cada parte del cociente, tanto en el numerador como en el denominador.
- 📊 El video muestra ejemplos prácticos de cómo realizar las multiplicaciones y combinaciones de términos al calcular la derivada.
- ⚠️ Se aconseja prestar atención a los signos al aplicar el negativo a las operaciones, especialmente al simplificar términos.
- 🔍 Se realizan operaciones de suma y resta de términos semejantes para simplificar el resultado final de la derivada.
- 💡 Se ofrece un ejercicio al final del video para que los espectadores practiquen el cálculo de derivadas de cocientes por su cuenta.
- 🧮 Se reitera que la práctica es clave para dominar el cálculo de derivadas, especialmente en funciones más complejas.
- 👍 Se invita a los espectadores a suscribirse, comentar y compartir el contenido para seguir aprendiendo sobre derivadas.
Q & A
¿Qué se enseña en este video?
-El video enseña cómo calcular la derivada de un cociente, utilizando la regla del cociente.
¿Cuál es la fórmula general para la derivada de un cociente?
-La fórmula es: (f'(g) * g - f * g') / g^2, donde f es el numerador y g es el denominador.
¿Qué método se sugiere para recordar la fórmula de la derivada de un cociente?
-Se sugiere recordar que la derivada se obtiene multiplicando el denominador por la derivada del numerador, menos el numerador por la derivada del denominador, todo dividido por el denominador al cuadrado.
¿Qué se hace primero al calcular la derivada?
-Primero, se debe encontrar la derivada del numerador y luego la del denominador.
¿Qué ejemplos se dan en el video para calcular derivadas?
-Se presentan ejemplos de binomios en el numerador y el denominador, mostrando cómo multiplicar y simplificar.
¿Cómo se manejan los signos negativos durante los cálculos?
-Se enfatiza que el signo negativo debe aplicarse a toda la operación cuando se usa la regla del cociente.
¿Qué se recomienda hacer después de calcular la derivada?
-Se recomienda combinar términos semejantes y simplificar la expresión final.
¿Qué ejercicio se deja para practicar al final del video?
-Se deja un ejercicio para que los espectadores calculen la derivada de otra función siguiendo el mismo método.
¿Qué recursos se ofrecen a los espectadores al final del video?
-Se invita a los espectadores a ver el curso completo de derivadas disponible en el canal y a interactuar con el contenido.
¿Cómo se puede seguir aprendiendo sobre derivadas después de ver este video?
-Los espectadores pueden suscribirse al canal y ver otros videos relacionados para profundizar en el tema.
Outlines

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードMindmap

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードKeywords

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードHighlights

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードTranscripts

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレード関連動画をさらに表示
Derivadas (Regla del cociente) 1

Derivada de un cociente | Reglas de derivación

Derivada de un producto o multiplicación de funciones. Cálculo diferencial

02. Derivative using definition as limit: Proof of formula

Aproximaciones. Uso de la diferencial.

CÓMO SE DERIVADA UNA FUNCIÓN PARAMÉTRICA - DERIVADA de FUNCIÓN PARAMÉTRICA #2
5.0 / 5 (0 votes)
