CUARTILES, DECILES Y PERCENTILES PARA DATOS NO AGRUPADOS
Summary
TLDREn este video se exploran las medidas de tendencia central, específicamente cuartiles, deciles y percentiles para datos no agrupados. Se explica cómo estos valores dividen un conjunto de datos ordenados en partes iguales: los cuartiles en cuatro, los deciles en diez y los percentiles en cien. A través de ejemplos prácticos, se detalla el proceso de cálculo de estas medidas, lo que permite a los estudiantes comprender mejor la distribución de datos y cómo obtener información valiosa de ellos. Este conocimiento es fundamental para el análisis estadístico efectivo.
Takeaways
- 📊 Los cuartiles, deciles y percentiles son valores que dividen una distribución de datos en partes iguales.
- 🔢 Los cuartiles dividen los datos en cuatro partes iguales, representando el 25% cada parte.
- 📏 Para calcular los cuartiles, primero se deben ordenar los datos de menor a mayor.
- ⚖️ La mediana (Q2) es también el cuartil 2 y se calcula como el valor central de un conjunto de datos.
- 📍 Q1 es el valor que se encuentra en la posición del 25% de los datos y Q3 en la posición del 75%.
- 🔟 Los deciles dividen los datos en diez partes iguales, cada una representando el 10% de la distribución.
- 🏷️ Para calcular un decil, se utiliza la fórmula Dk = k × (n + 1)/10, donde n es el total de datos.
- 💯 Los percentiles dividen los datos en 100 partes iguales, cada una representando el 1%.
- 📈 La fórmula para calcular un percentil es Pk = k × (n + 1)/100.
- ✨ Entender estos conceptos es fundamental para resumir y analizar conjuntos de datos en estadísticas.
Q & A
¿Qué son los cuartiles, deciles y percentiles?
-Son medidas estadísticas que dividen una distribución de datos en partes iguales, permitiendo entender la posición relativa de los valores dentro del conjunto de datos.
¿Cómo se definen los cuartiles?
-Los cuartiles son tres valores que dividen un conjunto de datos ordenados en cuatro partes iguales, donde cada parte representa el 25% de los datos.
¿Cuál es la fórmula para calcular el primer cuartil (Q1)?
-La fórmula para calcular Q1 es Q1 = (n + 1) / 4, donde n es el número total de datos.
¿Qué representa el cuartil 2 (Q2)?
-El cuartil 2, también conocido como la mediana, representa el valor que divide el conjunto de datos en dos partes iguales, es decir, el 50% de los datos se encuentra por debajo de este valor.
¿Qué son los deciles?
-Los deciles son los nueve valores que dividen un conjunto de datos ordenados en diez partes iguales, donde cada parte representa el 10% de los datos.
¿Cómo se calcula el quinto decil (D5)?
-La fórmula para D5 es D5 = 5(n + 1) / 10, donde n es el número total de datos. D5 también coincide con el cuartil 2, es decir, la mediana.
¿Qué son los percentiles?
-Los percentiles son los 99 valores que dividen un conjunto de datos ordenados en 100 partes iguales, donde cada parte representa el 1% de los datos.
¿Cómo se calcula un percentil Pk?
-La fórmula para calcular Pk es Pk = k(n + 1) / 100, donde k es el número del percentil y n es el total de datos.
¿Cuál es la diferencia entre cuartiles, deciles y percentiles?
-Los cuartiles dividen los datos en cuatro partes, los deciles en diez partes y los percentiles en cien partes, ofreciendo diferentes niveles de detalle sobre la distribución de los datos.
¿Por qué es importante calcular cuartiles, deciles y percentiles?
-Calcular estas medidas es crucial para analizar la distribución de datos, identificar tendencias y realizar inferencias estadísticas que pueden guiar la toma de decisiones.
Outlines

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードMindmap

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードKeywords

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードHighlights

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードTranscripts

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレード関連動画をさらに表示

MEDIDAS DE POSICIÓN (CUARTIL, DECIL, PERCENTIL) - DATOS AGRUPADOS
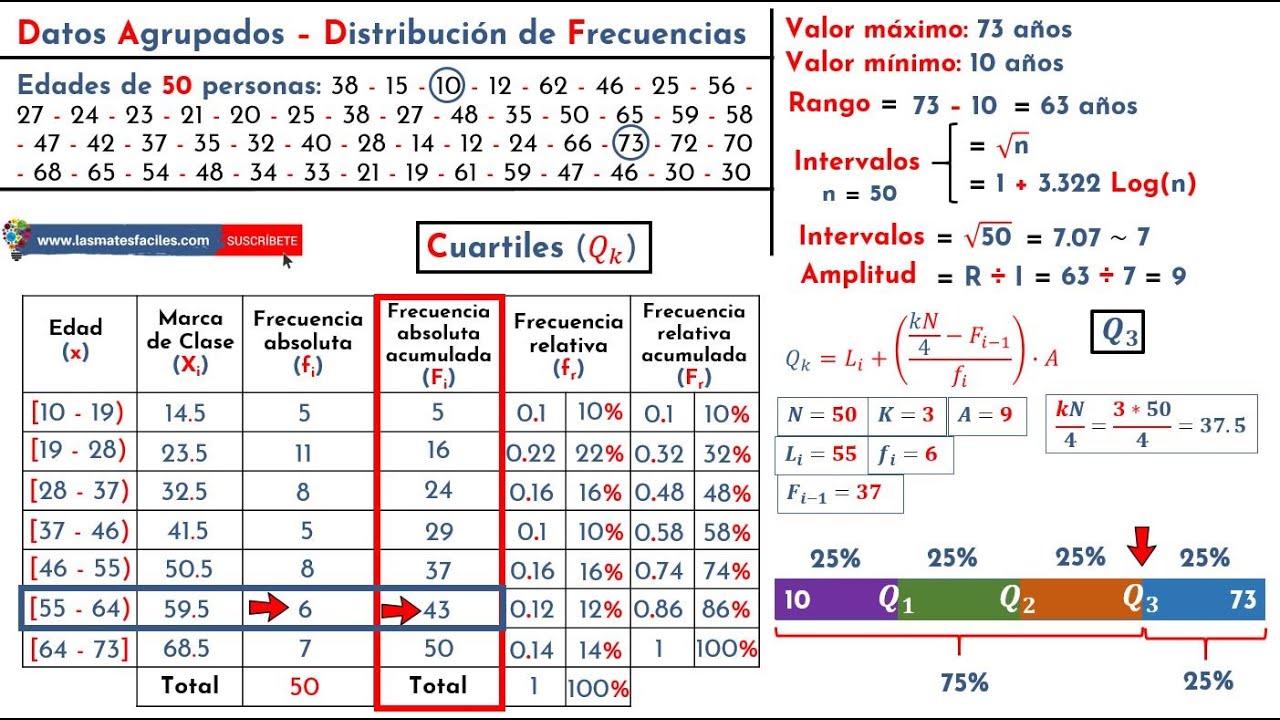
Cuartiles, Deciles y Percentiles - Datos Agrupados

Cuartiles, deciles y percentiles, datos agrupados, no agrupados, medidas de posición
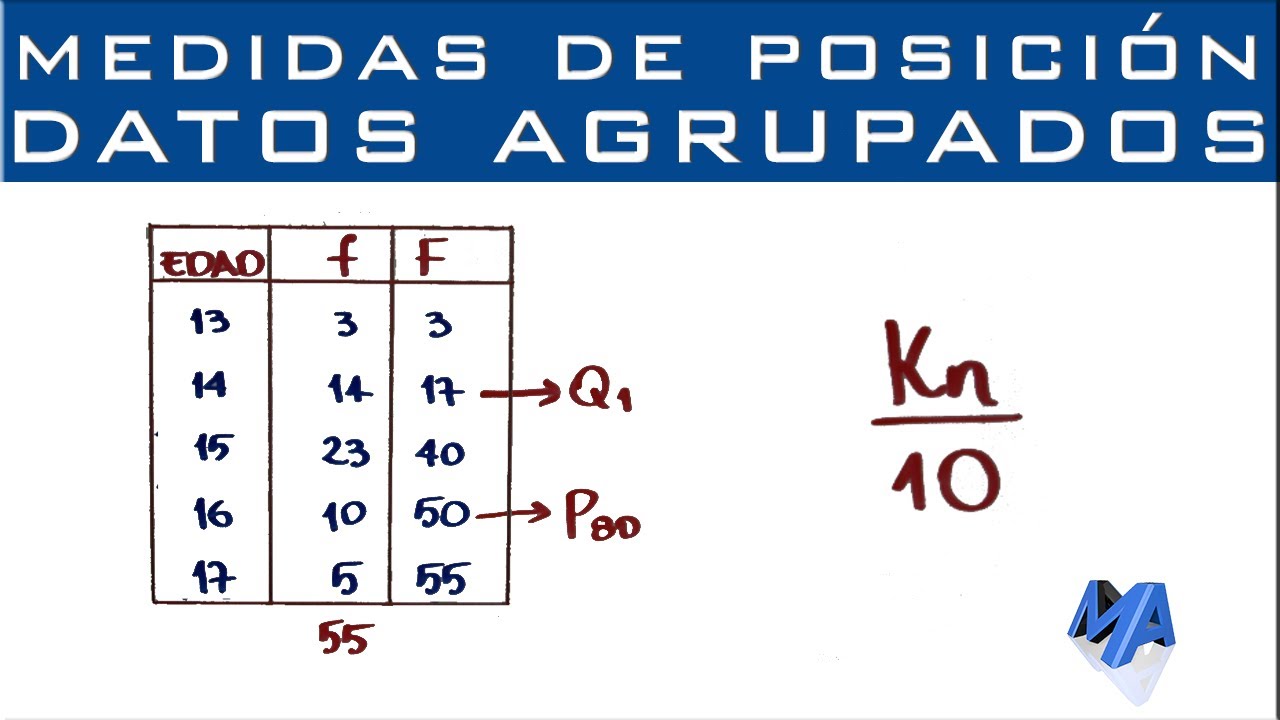
Cuartiles, Deciles y Percentiles | Datos agrupados puntualmente

Conceptos estadísticos básicos

Cuartiles, deciles y percentiles Definición e interpretaciones
5.0 / 5 (0 votes)
