One second to compute the largest Fibonacci number I can

Summary

このビデオは、フィボナッチ数の計算における効率的な手法を探る内容です。特に、Binetの公式を用いてフィボナッチ数を高速に計算する方法に焦点を当て、行列の対角化や高速フーリエ変換（FFT）の最適化技術を紹介します。これにより、数百万桁のフィボナッチ数の計算を1秒以内で達成する方法を説明しています。しかし、精度の限界とメモリ制約にも触れ、計算の限界を正直に明かすユーモラスな終わり方をしています。

Takeaways

• 😀 行列の高いべき乗を計算する際、2x2行列の計算は一般的に手作業では行わないが、特別な形の行列（対角行列）では比較的容易に計算できる。
• 😀 フィボナッチ数列を計算するための遷移行列は対角化可能であり、固有値を用いて行列の高いべき乗を効率的に計算できる。
• 😀 ビネットの公式を用いることで、フィボナッチ数を簡潔に表現できるが、公式には無理数が含まれる。
• 😀 コンピュータは実数を扱うことができるが、非常に大きな数値を扱う際の制約がある。
• 😀 フィボナッチ数の計算において、無理数を使わず、実際には有理数と√5を使った方が計算しやすい。
• 😀 √5を含む整数環（Z[√5]）を使うことで、計算の効率を高めることができ、特にフィボナッチ数を計算する際に有効。
• 😀 フィボナッチ数の計算を、(1 + √5)のn乗の係数を使って近似的に計算する方法が効率的である。
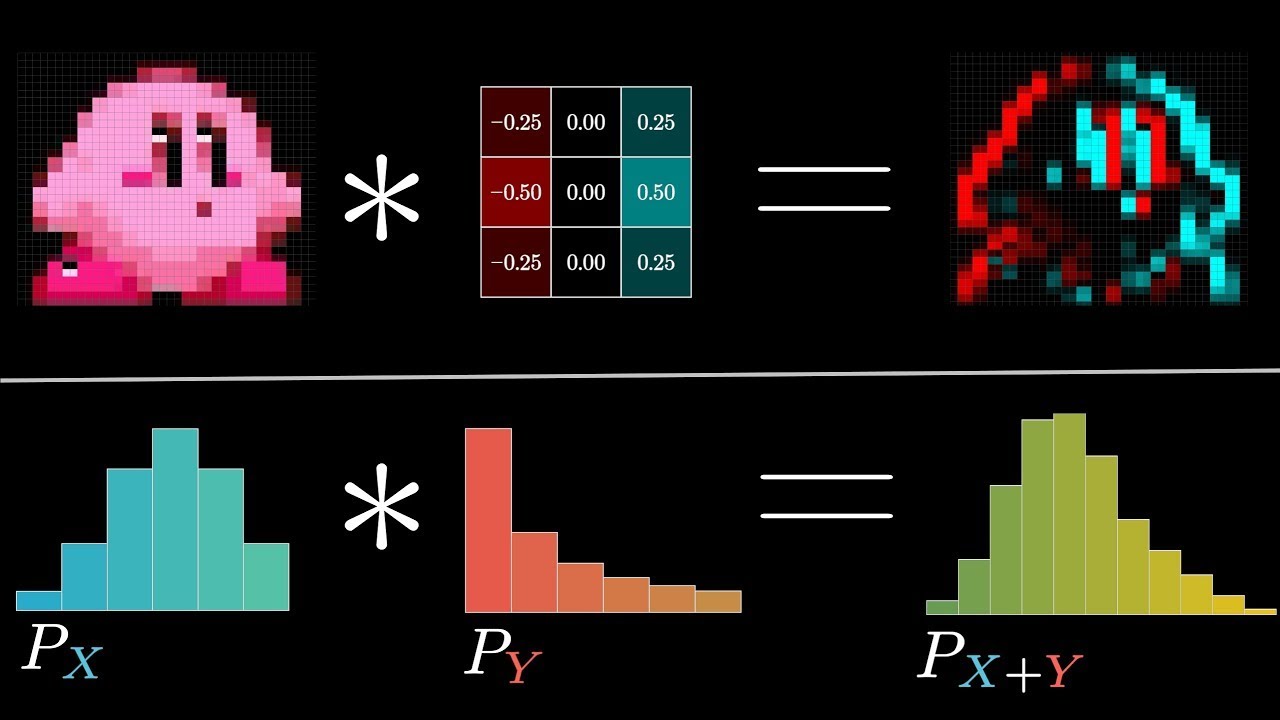
• 😀 数字をポリノミアル形式で表現することで、FFTを利用してフィボナッチ数を効率的に計算することが可能。
• 😀 最適化されたアルゴリズムを使うことで、1秒の制限内で400万番目のフィボナッチ数を計算できる。
• 😀 FFTアルゴリズムを使用する際には、計算精度に制約があり、特に非常に大きな数値の計算には限界がある。
• 😀 高速フーリエ変換（FFT）を使用したフィボナッチ数計算の際、精度が確保されるのは数十億桁までで、それを超えると精度に問題が生じることがある。

Q & A

フィボナッチ数列を計算するために使われる行列の種類は何ですか？

フィボナッチ数列を計算するためには、フィボナッチ遷移行列が使用されます。この行列は対角化可能で、特定の固有値（黄金比）を持ちます。

行列のべき乗を直接計算する代わりに、どのような方法が提案されていますか？

行列のべき乗を直接計算する代わりに、行列を対角化してからべき乗を計算し、その後逆対角化する方法が提案されています。これにより計算が効率的になります。

ビネの公式とは何ですか？

ビネの公式は、フィボナッチ数列のn番目の数を計算するための閉形式の式です。この式では、黄金比とその共役を使っています。

ビネの公式で使われる黄金比とは何ですか？

ビネの公式では、黄金比（φ）とその共役（-φの逆数）が使用されます。これらは無理数であり、フィボナッチ数列に関連しています。

コンピュータが無理数を正確に扱うのは難しい理由は何ですか？

無理数は精度を失うことがあるため、コンピュータでは扱うのが難しいです。しかし、ビネの公式では無理数を使う代わりに、有理数と√5を含む特定の数を使うことで計算が可能になります。

どのようにしてフィボナッチ数列を効率的に計算できますか？

フィボナッチ数列を効率的に計算するためには、FFT（高速フーリエ変換）を使った乗算アルゴリズムを使用し、2x2の行列ではなく、整数のペアを使うことでメモリを節約できます。

FFTを使う利点は何ですか？

FFTを使うことで、フィボナッチ数列の計算がO(n log n)の時間で効率的に行えます。また、FFTは大きな数を高速に乗算できるため、大きなフィボナッチ数も短時間で計算可能です。

計算精度に関する問題はどのように説明されていますか？

計算精度には限界があり、特に大きなフィボナッチ数列を扱う際に、精度が不足すると誤差が発生します。特にフーリエ変換を使用する場合、ビット精度が重要で、適切な精度が必要です。

どのくらいの大きさまでフィボナッチ数を計算できるのでしょうか？

ビデオで説明されている範囲では、4百万番目のフィボナッチ数まで計算できます。これを超えるとFFTアルゴリズムが失敗する可能性があります。

最終的に、どのような問題が明らかにされていますか？

最終的に、FFTアルゴリズムには限界があり、4百万番目のフィボナッチ数までの計算は成功するものの、それを超えると精度不足のため失敗する可能性があることが明らかにされています。