Dimensionless Parameters — Lesson 2
Summary
TLDRThis video discusses the significance of non-dimensional analysis in engineering, focusing on the Navier-Stokes equations. It explains how scaling models can predict system behavior under varying conditions by introducing non-dimensional variables, such as the Reynolds and Prandtl numbers. These parameters help characterize flow regimes, differentiating between laminar and turbulent flows. The lecture emphasizes the importance of dynamic similarity, enabling solutions from scaled models to apply to real-world systems. Through practical examples, it highlights the necessary adjustments in fluid properties to maintain similarity in experimental setups.
Takeaways
- 🔍 Takeaway 1: Non-dimensional analysis is essential for predicting how systems behave under various operating conditions using scaled models.
- ✈️ Takeaway 2: The approach of using governing equations in non-dimensional form can be applied to many fields, including aerodynamics and structural engineering.
- 📊 Takeaway 3: The incompressible Navier-Stokes equations assume constant density and exclude body forces, forming the basis for fluid flow analysis.
- 🔗 Takeaway 4: Introducing non-dimensional variables simplifies the equations, allowing for broader applicability across similar problems.
- ⚖️ Takeaway 5: The Reynolds number is a critical non-dimensional parameter that indicates the balance between inertial and viscous forces in fluid flow.
- 💧 Takeaway 6: Low Reynolds numbers signify laminar flow, while high Reynolds numbers indicate turbulent flow, characterized by chaotic fluid motion.
- 🔥 Takeaway 7: The Prandtl number compares viscous diffusion to thermal diffusion, influencing how heat transfers in fluids.
- 🌊 Takeaway 8: Other important non-dimensional numbers include the Brinkman number (viscous dissipation to conduction ratio) and the Froude number (inertial to gravitational forces ratio).
- 🚀 Takeaway 9: The Mach number indicates flow speed relative to the speed of sound, essential for analyzing compressible flows.
- 🔄 Takeaway 10: Achieving dynamic similarity across different models involves matching relevant dimensionless parameters, ensuring that one solution can represent multiple scenarios.
Q & A
What is the purpose of using scaled models in preliminary design analysis?
-Scaled models are used to predict how full-size bodies would behave under specific operating conditions, allowing for better understanding and analysis of systems like airplanes and buildings.
What are the Navier-Stokes equations, and why are they important?
-The Navier-Stokes equations describe the motion of fluid substances. They are important because they provide fundamental insights into fluid dynamics and help analyze how fluids behave under various conditions.
How are non-dimensional variables introduced into the Navier-Stokes equations?
-Non-dimensional variables are introduced by dividing dimensional terms by reference values, such as characteristic length and density, to create non-dimensional forms of the equations.
What is the Reynolds number, and what does it signify?
-The Reynolds number is the ratio of inertial forces to viscous forces in a fluid flow. It helps determine the flow regime, indicating whether the flow is laminar (low Reynolds number) or turbulent (high Reynolds number).
What characterizes laminar and turbulent flows?
-Laminar flows, which occur at low Reynolds numbers, are dominated by viscous forces and move smoothly. In contrast, turbulent flows at high Reynolds numbers are dominated by inertial forces and exhibit chaotic, energetic mixing.
What role does the Prandtl number play in fluid dynamics?
-The Prandtl number represents the ratio of viscous diffusion to thermal diffusion. It helps in understanding heat transfer mechanisms in fluids, indicating whether heat transfer occurs primarily through conduction or convection.
What is dynamic similarity, and why is it important in fluid dynamics?
-Dynamic similarity occurs when relevant dimensionless parameters, such as the Reynolds number, are the same for different cases. It is crucial because it ensures that solutions for scaled models can be applied to full-scale systems.
How can engineers achieve dynamic similarity when testing scaled models?
-Engineers can achieve dynamic similarity by adjusting parameters like fluid density, viscosity, and velocity to ensure that the Reynolds number for the model matches that of the full-scale case.
What is the significance of the Froude number in fluid dynamics?
-The Froude number is the ratio of inertial forces to gravitational body forces. It is significant in naval architecture and is used to analyze water wave motion and ship resistance.
What is the Mach number, and how does it relate to flow speed?
-The Mach number is the ratio of flow speed to the speed of sound. It helps characterize compressible flows, indicating whether the flow is subsonic (Mach < 1) or supersonic (Mach > 1).
Outlines

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードMindmap

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードKeywords

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードHighlights

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードTranscripts

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレード関連動画をさらに表示

LECTURE NOTES: AIRCRAFT AERODYNAMICS I, CHAPTER I, PART 3

LECTURE NOTES: AIRCRAFT AERODYNAMICS I, CHAPTER I, PART 1
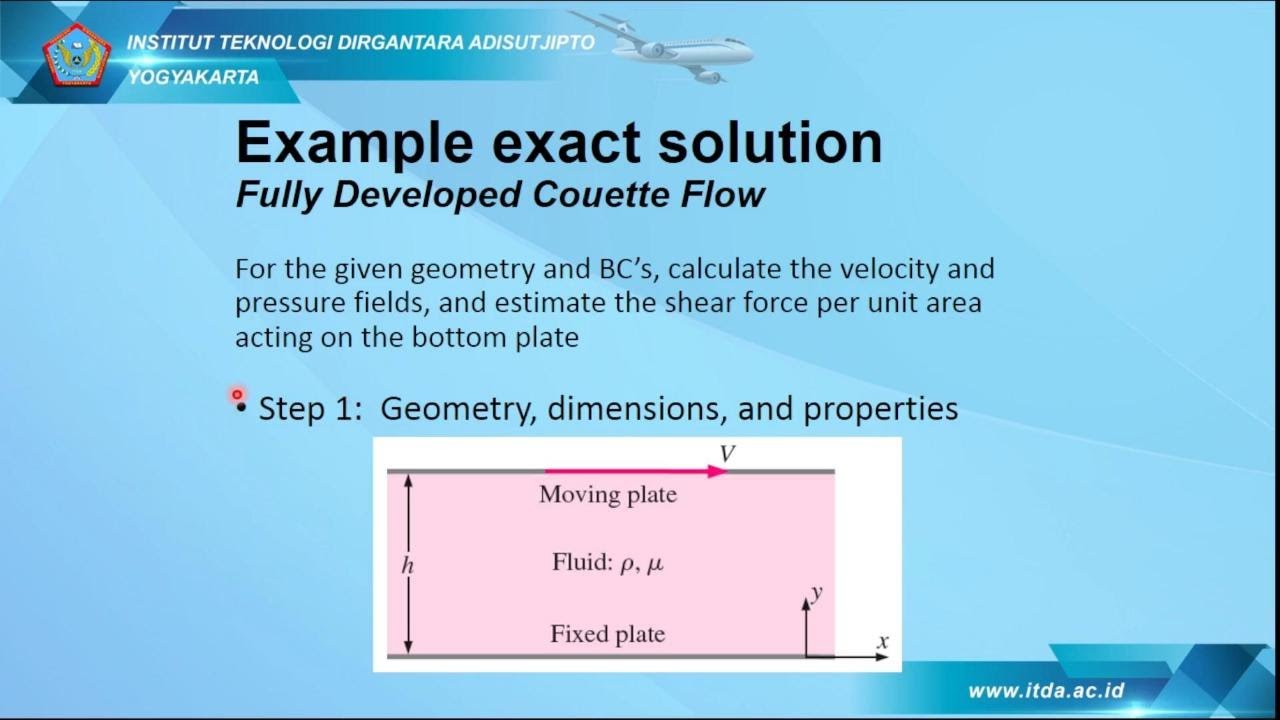
LECTURE NOTES: AIRCRAFT AERODYNAMICS I, CHAPTER I, PART 4

The million dollar equation (Navier-Stokes equations)
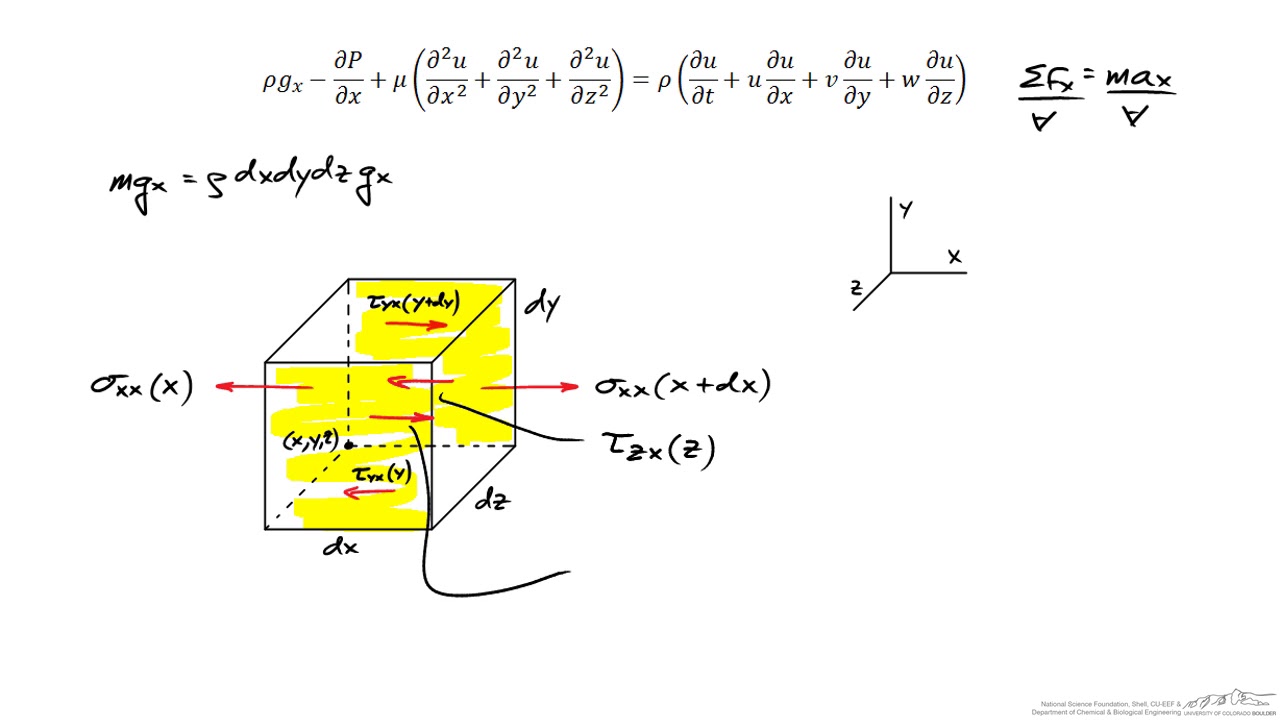
Description and Derivation of the Navier-Stokes Equations

How to derive equation using Dimension | Unit 1 Measurements- #TP11 06
5.0 / 5 (0 votes)
