Turunan fungsi trigonometri
Summary
TLDRThis video offers a detailed explanation of trigonometric function derivatives, aimed at helping viewers grasp key concepts. It begins by reviewing fundamental trigonometric derivative formulas, such as the derivatives of sine and cosine. The presenter solves multiple problems step-by-step, starting with simple examples and progressing to more complex cases, including product and quotient rules. Additionally, the video emphasizes the importance of understanding trigonometric identities for simplifying answers. Overall, the tutorial provides practical tips for mastering trigonometric derivatives, ensuring the audience can easily follow along.
Takeaways
- 📘 The video focuses on explaining derivatives of trigonometric functions, particularly their basic formulas and applications.
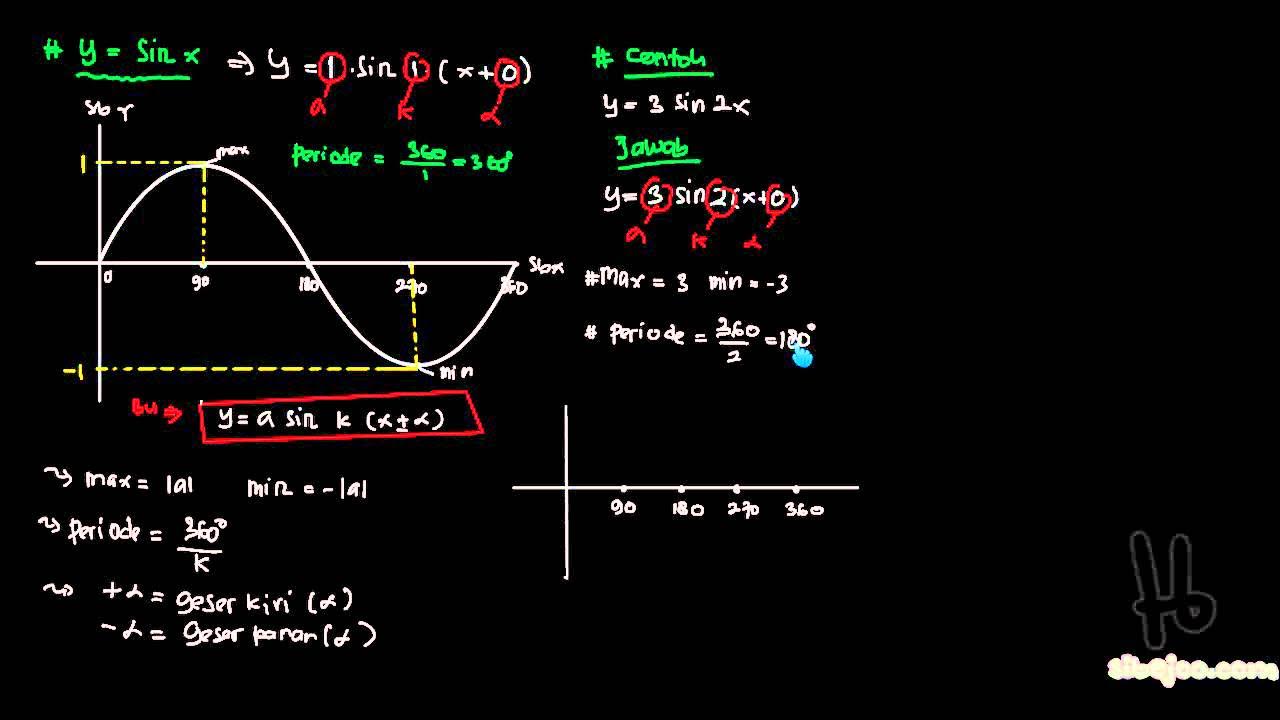
- 📝 The first basic derivative discussed is that of sine (sin), which becomes cosine (cos). The derivative of cosine is negative sine (-sin).
- 🔢 Example 1: For the function f(x) = 4cos(x), the derivative is f'(x) = -4sin(x).
- 💡 Example 2: For the function f(x) = 2sin(3x + 5), the derivative is calculated by applying both the chain rule and trigonometric rules, leading to f'(x) = 6cos(3x + 5).
- ➕ Example 3: The derivative of a combined function like f(x) = 2sin(x) + 3cos(x) is calculated by finding the derivative of each term separately.
- ⚙️ Example 4 introduces the product rule for derivatives using the function f(x) = 2sin(3x) * cos(x), which involves differentiating each part of the product.
- 📉 Simplification of complex trigonometric expressions is crucial, and the video uses identities like cos(a)cos(b) and sin(a)sin(b) to simplify results.
- 📏 Example 5 demonstrates the quotient rule with the function f(x) = (1 - sin(x)) / cos(x), emphasizing the importance of using trigonometric identities.
- 📚 The video stresses the importance of understanding trigonometric identities, such as sin^2(x) + cos^2(x) = 1, for simplifying derivative expressions.
- 🔗 The final example covers the chain rule in depth, particularly for functions with nested trigonometric expressions like f(x) = sin^3(2x - 1).
Q & A
What is the basic formula for the derivative of sine and cosine functions?
-The derivative of sine (sin x) is cosine (cos x), and the derivative of cosine (cos x) is negative sine (-sin x).
How do you find the derivative of the function f(x) = 4 cos(x)?
-To find the derivative of f(x) = 4 cos(x), keep the constant 4 in front and differentiate cos(x), which results in -sin(x). The final derivative is f'(x) = -4 sin(x).
What steps are involved in finding the derivative of f(x) = 2 sin(3x + 5)?
-First, keep the constant 2 in front, then differentiate the inner function 3x + 5, which gives 3. Finally, differentiate sin(3x + 5) to get cos(3x + 5). The derivative is f'(x) = 2 * 3 * cos(3x + 5) = 6 cos(3x + 5).
How can you calculate the derivative of f(x) = 2 sin(x) + 3 cos(x)?
-Differentiate each term separately. The derivative of 2 sin(x) is 2 cos(x), and the derivative of 3 cos(x) is -3 sin(x). So, the derivative is f'(x) = 2 cos(x) - 3 sin(x).
What is the product rule, and how is it applied to the function f(x) = 2 sin(3x) cos(x)?
-The product rule states that for two functions u and v, the derivative of their product is u'v + uv'. For f(x) = 2 sin(3x) cos(x), treat u = 2 sin(3x) and v = cos(x). First, differentiate u to get 6 cos(3x), and differentiate v to get -sin(x). Applying the product rule, f'(x) = 6 cos(3x) cos(x) - 2 sin(3x) sin(x).
How do you simplify trigonometric expressions using identities?
-Trigonometric identities, such as cos(A + B) = cos(A)cos(B) - sin(A)sin(B) and cos(A - B) = cos(A)cos(B) + sin(A)sin(B), are used to simplify complex expressions. For example, 6 cos(3x) cos(x) can be simplified using the identity 2 cos(A) cos(B) = cos(A + B) + cos(A - B).
How do you approach derivatives involving trigonometric functions in fraction form, like f(x) = (1 - sin(x)) / cos(x)?
-To differentiate f(x) = (1 - sin(x)) / cos(x), use the quotient rule, where the derivative of a fraction u/v is (u'v - uv') / v². First, differentiate the numerator (1 - sin(x)) to get -cos(x), and the denominator (cos(x)) to get -sin(x). Apply the quotient rule to get f'(x) = (cos²(x) + sin(x)) / cos²(x).
What is the chain rule, and how is it applied to functions like f(x) = sin³(2x - 1)?
-The chain rule states that if a function is composed of other functions, you differentiate the outer function and then multiply by the derivative of the inner function. For f(x) = sin³(2x - 1), rewrite it as (sin(2x - 1))³. First, differentiate the outer function (3sin²(2x - 1)) and then multiply by the derivative of the inner function, which is cos(2x - 1) * 2. The final derivative is 6 sin²(2x - 1) cos(2x - 1).
How do you handle higher-degree trigonometric functions like f(x) = sin³(x)?
-For higher-degree trigonometric functions like sin³(x), use the chain rule. First, write it as (sin(x))³. Then, differentiate the outer function (3sin²(x)) and multiply by the derivative of sin(x), which is cos(x). The result is 3 sin²(x) cos(x).
What are some key trigonometric identities needed to simplify derivative problems?
-Important trigonometric identities include sin²(x) + cos²(x) = 1, 1 - sin²(x) = cos²(x), and the angle sum and difference formulas like cos(A ± B) = cos(A)cos(B) ∓ sin(A)sin(B). These help simplify expressions in derivatives and integrals involving trigonometric functions.
Outlines

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードMindmap

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードKeywords

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードHighlights

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードTranscripts

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレード5.0 / 5 (0 votes)