Limits in Calculus: Definition & Meaning. What is a Limit?
Summary
TLDRThis script offers a comprehensive explanation of the concept of limits in calculus. It begins with a layman's approach, explaining how limits work for smooth, continuous functions by plugging in the value of 'a'. The script then transitions to a more rigorous mathematical definition, introducing the symbols 'Delta' and 'Epsilon' to represent infinitesimally small distances. It visually describes how as 'X' approaches 'a', the function 'f(x)' approaches 'L', using graphical illustrations to clarify. The script concludes by demystifying the formal mathematical definition found in textbooks, making the abstract concept of limits more tangible.
Takeaways
- 📘 The limit of a function f(x) as x approaches a number a is defined as a value L, which the function gets arbitrarily close to without actually reaching it.
- 📐 In layman's terms, a limit is the value a function approaches as the input gets infinitely close to a certain point, without the input actually being that point.
- 📊 Mathematically, limits are described using the concept of 'delta' (Δ) and 'epsilon' (ε), which are small numbers representing the proximity of x to a and f(x) to L, respectively.
- 🔍 The definition of a limit is rigorous and involves the idea that for any small distance from a (denoted by Δ), there exists a corresponding small distance from L (denoted by ε) for the function's value.
- 📉 The concept of approaching a limit can be visualized graphically, where x values close to a result in f(x) values close to L, regardless of approaching from the left or right.
- 📌 The definition of a limit is foundational in calculus and is used to prove the existence of limits under certain conditions, which is essential for understanding more complex calculus concepts.
- 🔢 The mathematical framework for limits involves the idea that if the distance between x and a can be made arbitrarily small (i.e., less than any given positive Δ), then the distance between f(x) and L can also be made arbitrarily small (i.e., less than any given positive ε).
- 📝 The script emphasizes that understanding the formal definition of a limit is crucial for reading and comprehending more advanced mathematical theorems and definitions in calculus.
- 🎯 The practical application of limits in calculus often involves using limit laws or rules to solve problems, which builds upon the foundational understanding of what a limit represents.
- 📚 The video script serves as an educational resource to demystify the concept of limits for students, providing both a high-level understanding and the detailed mathematical framework necessary for deeper study.
Q & A
What is the basic concept of a limit in mathematics?
-The basic concept of a limit in mathematics is that the value of a function approaches a certain value L as the input x approaches a certain value a, even though the function may not be defined at x = a itself.
Why is it important to approach a limit without actually reaching the value 'a'?
-Approaching a limit without reaching the value 'a' is important because it allows for the consideration of the behavior of the function around the point 'a', including cases where the function may not be defined at 'a', ensuring that the limit can be discussed in a broader context.
What is the role of the small number 'Delta' in the definition of a limit?
-The small number 'Delta' in the definition of a limit represents a range of values around 'a' that x can approach. It is used to define how close x can get to 'a' without actually being equal to 'a', thus allowing for the concept of infinitesimally close values.
How does the value 'Epsilon' relate to the definition of a limit?
-The value 'Epsilon' (ε) is used to measure how close the function's value can get to the limit L. As 'Delta' becomes smaller, 'Epsilon' also becomes smaller, indicating that the function's value gets arbitrarily close to L as x gets close to 'a'.
What does it mean to say that a function is 'smooth and continuous'?
-A function is 'smooth and continuous' if it has no breaks, jumps, or cusps. It implies that the function can be drawn without lifting the pen from the paper, and it is differentiable within the interval being considered.
Why is it necessary to use absolute values in the mathematical definition of a limit?
-Absolute values are used in the definition of a limit to ensure that the approach from both sides of 'a' (from the left and the right) is accounted for. It disregards the direction of approach, focusing only on the magnitude of the difference between the function's value and the limit.
How does the concept of a limit relate to the graphical representation of a function?
-In the graphical representation, a limit is shown as the value that the function's graph approaches as the input x gets infinitely close to 'a'. This is visualized as the graph getting closer and closer to a horizontal line at the value L, without necessarily touching it at x = a.
What is the significance of the phrase 'for every positive number Epsilon' in the definition of a limit?
-The phrase 'for every positive number Epsilon' signifies that no matter how small a positive distance from L one chooses, there exists a correspondingly small distance from 'a' (measured by Delta) such that the function's value will be within that small distance of L.
Can you provide an example of a function that is not smooth and continuous?
-An example of a function that is not smooth and continuous is a step function, such as the Heaviside function, which has a sudden jump at a certain point, or a function with a cusp, like f(x) = |x| at x = 0.
What are some practical implications of understanding limits in calculus?
-Understanding limits is fundamental in calculus for evaluating the behavior of functions, determining slopes of tangents, computing areas under curves, and understanding the convergence of infinite series, among other applications.
Outlines

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードMindmap

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードKeywords

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードHighlights

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードTranscripts

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレード関連動画をさらに表示
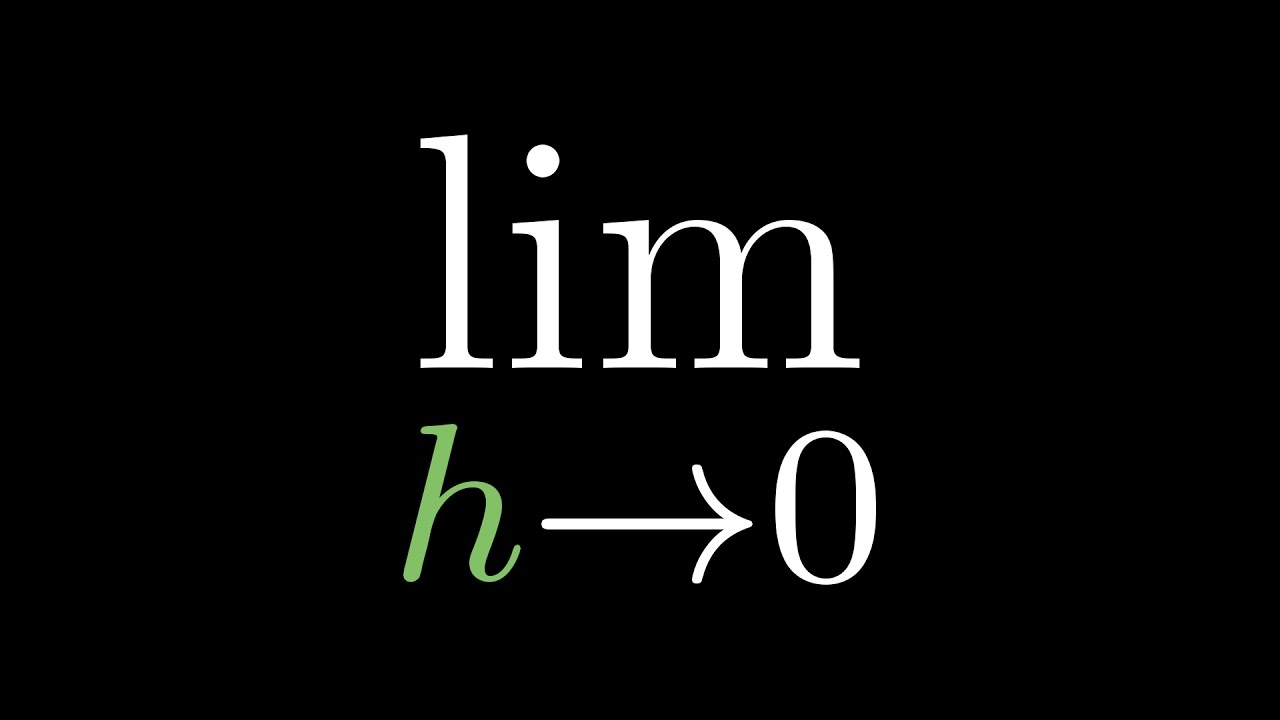
Limits, L'Hôpital's rule, and epsilon delta definitions | Chapter 7, Essence of calculus

Limit of a Function using a Graph - Basic/Differential Calculus

Cálculo: Introdução e Noção Intuitiva de Limites (Aula 1 de 15)

Calculus 1 - Introduction to Limits

Jika lim x->-3 (x^2+4x+3)/(x+3)=a-1,nilai a adalah...

Calculus - Introduction to Calculus
5.0 / 5 (0 votes)
