Unveiling The Remarkable Discovery Of Pi By A Genius - Prepare To Be Amazed!
Summary
TLDRIn this fun and educational video, the host explains how Archimedes discovered the value of pi using a simple method with a wheel. The video demonstrates how to measure the circumference of a circle and its relationship to the diameter using a homemade wheel from a cereal box. By rolling the wheel and marking its rotation, the presenter shows that the ratio of the circumference to the diameter is approximately 3.14, which is pi. The process highlights how Archimedes made this groundbreaking discovery with basic tools and ingenuity.
Takeaways
- 🌀 Archimedes discovered that the circumference of a circle equals 3.14 times the diameter, which is now known as Pi (π).
- 🎨 The video demonstrates how to visually calculate Pi using a wheel and a straight path.
- ✂️ The creator uses a cardboard cutout from a cereal box to replicate a wheel for the experiment.
- 📏 Archimedes used a simple cartwheel in his experiment, but modern tools like rulers and cutting tools make it easier.
- 🔴 The creator marks an arrow on the wheel to track one complete rotation, allowing them to measure the circumference.
- 🧮 The experiment shows that it takes about 3.14 diameters for the wheel to complete one full rotation, visually explaining Pi.
- 📐 The formula for circumference is confirmed as 2πr (2 times Pi times the radius).
- 📊 The calculated circumference using Pi and the radius matches the measured circumference, confirming the accuracy of the relationship.
- 📕 The creator refers to a book about Archimedes, highlighting his contributions beyond Pi, including the invention of the death ray.
- ✏️ The video encourages viewers to keep practicing math and drawing, with a call to action to subscribe and explore more educational content.
Q & A
Who was the first person to work out the value of pi?
-Archimedes was the first person to work out the value of pi by analyzing the relationship between a circle's circumference and its diameter.
How did Archimedes calculate the value of pi?
-Archimedes used a wheel, much like a cartwheel, and rolled it along a surface to measure how many times its diameter fit into its circumference. He found that it took about 3.14 diameters to complete one full rotation.
What is the mathematical formula involving pi to calculate the circumference of a circle?
-The formula is C = 2πr, where C is the circumference and r is the radius of the circle.
Why is the number pi approximately 3.14?
-Pi represents the ratio of a circle’s circumference to its diameter, which is approximately 3.14. This relationship was first observed by Archimedes and later refined through more precise calculations.
What simple materials did the presenter use to demonstrate the concept of pi?
-The presenter used a piece of cardboard, scissors, glue, and a circular object like a glass or jar to create a simple wheel for the demonstration.
How did the presenter use the wheel to demonstrate the value of pi?
-The presenter marked a point on the wheel, rolled it along a flat surface, and measured how many times the wheel’s diameter fit into its full rotation. The distance was approximately 3.14 times the diameter.
How can we apply the formula 2πr to find the circumference of a circle?
-First, measure the radius of the circle (r). Then multiply it by 2 and by pi (3.14) to find the circumference. For example, if the radius is 34mm, the circumference would be 213.52mm.
What tools did the presenter use to ensure accuracy in the demonstration?
-The presenter used a compass to draw a precise circle and a calculator to verify the result of the circumference formula.
Why is it important to understand where the value of pi comes from?
-Understanding the origin of pi helps clarify its practical applications in mathematics and geometry, showing that it’s not just an arbitrary number but derived from real-world observations.
How did the presenter connect the demonstration to Archimedes' original method?
-The presenter highlighted how Archimedes used a wheel in a similar manner, rolling it along a surface to measure the relationship between the circumference and the diameter, a method mirrored in the cardboard demonstration.
Outlines

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードMindmap

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードKeywords

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードHighlights

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードTranscripts

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレード関連動画をさらに表示

BERMATEMATIKA #17: Dari Mana Asalnya Hampiran π ≈ 22/7?

Comprimento da circunferência e o número pi

Luas Permukaan Prisma dan Tabung Hal 213-215 Bab 6 Kelas 7 Kurikulum Merdeka

Praktikum Kincir Air | SaBiKum | Eksperimen Sains | DIY
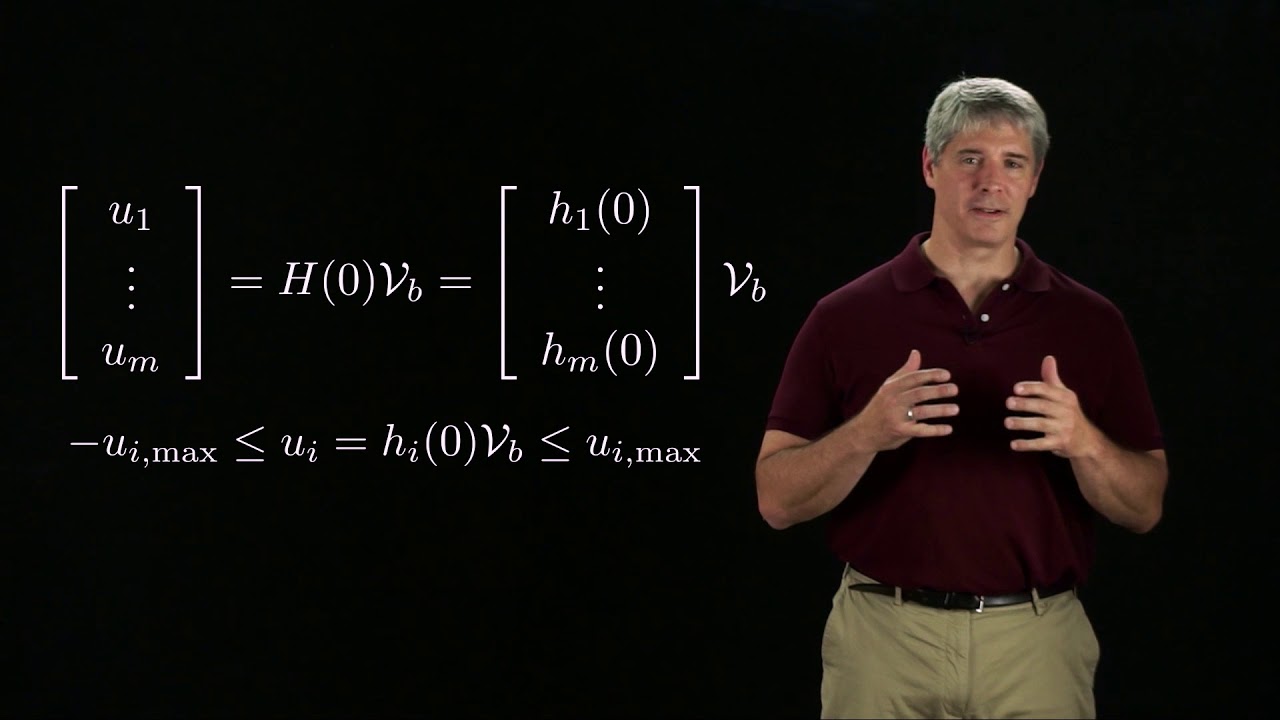
Modern Robotics, Chapter 13.2: Omnidirectional Wheeled Mobile Robots (Part 2 of 2)

The Discovery That Transformed Pi
5.0 / 5 (0 votes)
