Derivadas algebraicas y concepto preliminar de una diferencial - ROMATH
Summary
TLDREl video trata sobre el concepto de derivadas en cálculo diferencial, explicando cómo calcular la pendiente de una recta tangente a una curva en un punto específico. Utilizando la notación de Leibniz y fórmulas básicas de derivación, se ejemplifica el proceso de derivar funciones como x^2 y aplicar la regla de la cadena. Además, se muestra cómo las derivadas permiten determinar ecuaciones de rectas tangentes y se introduce el uso de exponentes fraccionarios para funciones más complejas, destacando la importancia de las derivadas en la geometría analítica y la comprensión de curvas.
Takeaways
- 📐 La función primitiva, como \( f(x) = x^2 \), permite graficar la relación en el plano cartesiano al sustituir valores y calcular puntos.
- 🔍 Para encontrar la función de una recta tangente a una curva, se necesita la pendiente, la cual se puede obtener a partir de la derivada de la función.
- 📘 La derivada es una función que permite calcular la pendiente de cualquier recta tangente a la curva en cualquier punto, usando la notación de Leibniz.
- 🔄 La derivada de una función con respecto a una variable independiente se relaciona con la misma variable independiente, y permite calcular la pendiente de la recta tangente.
- 📐 La derivada de \( x^2 \) es \( 2x \), lo cual se puede obtener aplicando las fórmulas de cálculo diferencial y la notación de Leibniz.
- 📈 La pendiente de la recta tangente en un punto específico de la curva se calcula sustituyendo el valor de \( x \) en la derivada de la función.
- 📊 La ecuación de la recta tangente se obtiene a partir de la pendiente y un punto por donde pasa, usando la fórmula de geometría analítica.
- 🔢 La derivada de una función compleja, como \( x^{5/3} \), se calcula aplicando reglas de derivación y la regla de la cadena, resultando en \( 5x^{2/3} \).
- 📘 La derivada de una función a una fracción de exponente, como la raíz séptima de \( x^4 \), se obtiene aplicando la regla de los exponentes fraccionarios, resultando en \( \frac{4}{7}x^{-3/7} \).
- 🔄 La diferencial de una función, representada como \( dy \), está relacionada con la derivada y se utiliza para calcular las pendientes de las rectas tangentes a la curva.
Q & A
¿Qué es una función primitiva y cómo se relaciona con la derivada?
-Una función primitiva es una función que permite graficar en el plano cartesiano. La relación con la derivada es que esta última permite calcular la pendiente de cualquier recta tangente a la curva de la función primitiva en cualquier punto.
¿Cómo se calcula la derivada de una función usando la notación de Leibniz?
-La derivada de una función usando la notación de Leibniz se calcula utilizando la fórmula 'dy/dx', donde 'dy' es la diferencial de la función y 'dx' es la diferencial de la variable independiente.
¿Qué significa 'f prima' en el contexto de la derivada?
-'f prima' se refiere a la derivada de una función 'f', es decir, la función que permite calcular la pendiente de la recta tangente a la curva de 'f' en cualquier punto.
¿Cómo se calcula la derivada de una función con respecto a x si la función está dada como 'x al cuadrado'?
-La derivada de una función 'x al cuadrado' con respecto a x se calcula utilizando la fórmula de la derivada de una potencia, que es 'n * x^(n-1)'. En este caso, 'n' es 2, por lo que la derivada es '2 * x^(2-1)', que es igual a '2x'.
¿Qué es la derivada de la función 'x al cuadrado' y cómo se utiliza para encontrar la pendiente de la recta tangente en un punto específico?
-La derivada de la función 'x al cuadrado' es '2x'. Para encontrar la pendiente de la recta tangente en un punto específico, se evalúa la derivada en el valor de x de ese punto.
¿Cómo se determina la ecuación de una recta tangente a una función dada un punto y la pendiente?
-La ecuación de una recta tangente se determina utilizando la fórmula 'y - y1 = m(x - x1)', donde 'm' es la pendiente y '(x1, y1)' son las coordenadas del punto de tangencia.
¿Qué es la regla de la cadena en el contexto de la derivación y cómo se aplica?
-La regla de la cadena es una técnica de derivación utilizada cuando se tiene una función compuesta de dos o más funciones. Se aplica derivando la función exterior y luego multiplicando por la derivada de la función interior.
¿Cómo se calcula la derivada de una función que contiene una raíz y una potencia, como 'x^(4/7)'?
-Para calcular la derivada de una función como 'x^(4/7)', se utiliza la regla de las potencias y la regla de la cadena. La derivada es '(4/7) * x^(4/7 - 1)', que simplifica a '(4/7) * x^(-3/7)'.
¿Qué significa 'diferencial' en el contexto de la derivada y cómo se relaciona con la pendiente de la recta tangente?
-El diferencial en el contexto de la derivada es una medida de la variación de una función con respecto a una variación en la variable independiente. Se relaciona con la pendiente de la recta tangente porque la derivada, que es el coeficiente del diferencial, representa la pendiente de la tangente en un punto específico.
¿Cómo se utiliza la derivada para encontrar la recta tangente a una curva dada una función y un punto?
-Para encontrar la recta tangente a una curva dada una función y un punto, se calcula la derivada de la función para obtener la pendiente en el punto de interés y luego se utiliza la fórmula de la recta para determinar la ecuación de la tangente.
Outlines

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードMindmap

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードKeywords

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードHighlights

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードTranscripts

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレード関連動画をさらに表示

Concepto de la derivada explicado fácil y sencillo
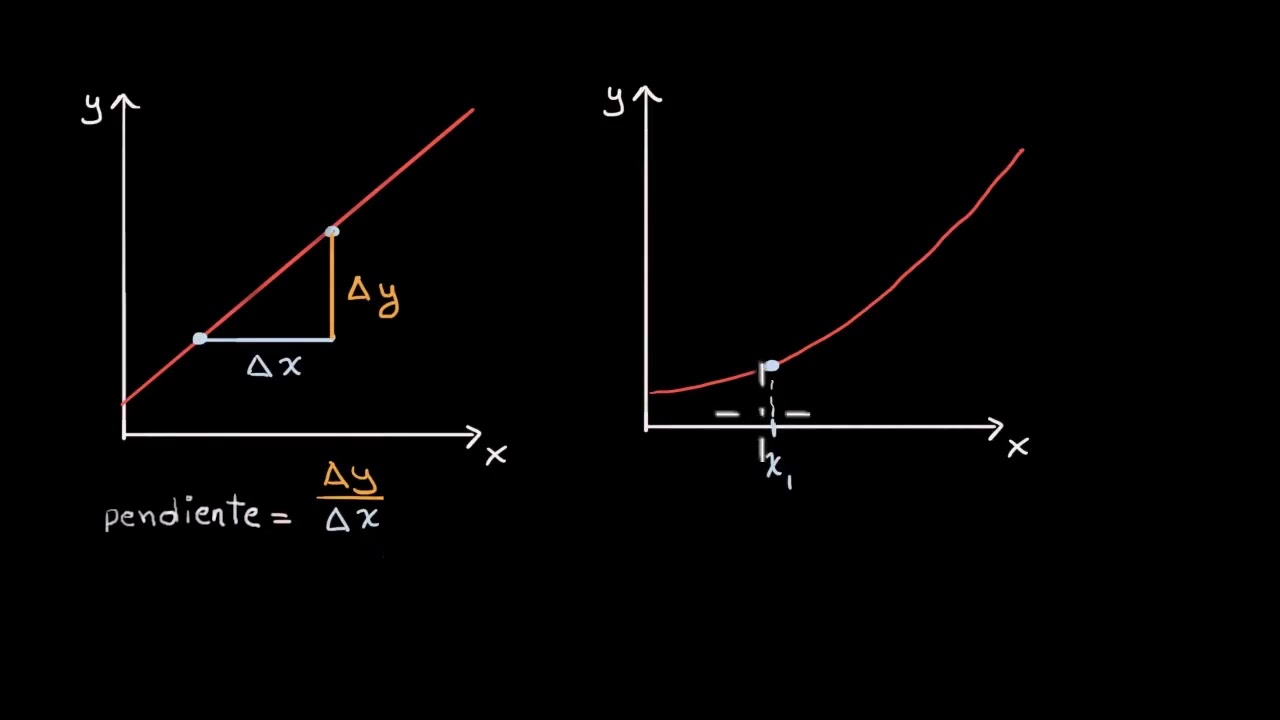
El concepto de derivada | Khan Academy en Español

Pendiente de la recta tangente a una curva | Introducción a la derivada

INTERPRETACIÓN GEOMÉTRICA DE LA DERIVADA, CÁLCULO DIFERENCIAL

✅ LA INTERPRETACIÓN GEOMÉTRICA DE LA DERIVADA | ANÁLISIS MATEMÁTICO 💯

El problema de la recta tangente.
5.0 / 5 (0 votes)
