Solving Quadratic Equations by Factoring @MathTeacherGon - Grade 9 Math
Summary
TLDRIn this educational video, the teacher introduces viewers to solving quadratic equations by factoring, a method applicable to various equations. The tutorial covers six different equations, demonstrating common monomial factoring for the first two and difference of squares for the third and fourth. The fifth equation showcases solving a trinomial equation by factoring, while the sixth involves finding factors of a quadratic equation with a negative linear coefficient. The video encourages practice and interaction, inviting viewers to solve additional equations and engage with the content.
Takeaways
- 📚 The video covers solving quadratic equations by factoring, a method to find solutions for various quadratic equations.
- 🔢 The first two equations are solved using common monomial factoring, which involves identifying common factors in the terms of the equations.
- 📝 For the equation 3x^2 - 9x = 0, the common factor is 3x, leading to the factored form (3x)(x - 3) = 0, with solutions x = 0 and x = 3.
- 📘 The second equation, 5x^2 - 20x = 0, is factored using 5x as the common factor, resulting in (5x)(x - 4) = 0, with solutions x = 0 and x = 4.
- 🔍 The video introduces the difference of squares pattern for equations like x^2 - 16 = 0, which factors into (x + 4)(x - 4) = 0, yielding solutions x = -4 and x = 4.
- 📐 The square root method is used for equations like x^2 - 64 = 0, factoring into (x + 8)(x - 8) = 0, with solutions x = -8 and x = 8.
- 🔑 The video demonstrates solving trinomial equations by factoring, choosing factors that multiply to the constant term and add up to the linear coefficient.
- 🧩 For the trinomial equation x^2 - 15x + 20 = 0, the factors (x - 5)(x - 4) are chosen, resulting in solutions x = 5 and x = 4.
- 📉 The last example, x^2 - 7x + 12 = 0, uses factors (x - 4)(x - 3), leading to solutions x = 4 and x = 3.
- 👨🏫 The instructor encourages viewers to practice factoring and solving quadratic equations, offering additional problems for practice and inviting engagement through comments.
Q & A
What is the main topic discussed in the video?
-The main topic discussed in the video is solving quadratic equations by factoring.
How many different quadratic equations are provided in the video to be solved by factoring?
-Six different quadratic equations are provided in the video to be solved by factoring.
What is the first method of factoring introduced in the video?
-The first method of factoring introduced in the video is common monomial factoring.
For the equation 3x^2 - 9x = 0, what is the common monomial factor?
-For the equation 3x^2 - 9x = 0, the common monomial factor is 3x.
What are the solutions for the equation 3x^2 - 9x = 0 after factoring?
-The solutions for the equation 3x^2 - 9x = 0 are x = 0 and x = 3.
How does the video approach solving quadratic equations that are in the form of a difference of squares?
-The video approaches solving quadratic equations in the form of a difference of squares by using the pattern a^2 - b^2 = (a + b)(a - b).
What is the pattern used to factor equations like x^2 - 16 = 0?
-The pattern used to factor equations like x^2 - 16 = 0 is the difference of squares, which is x^2 - 4^2 = (x + 4)(x - 4).
What are the solutions for the equation x^2 - 16 = 0?
-The solutions for the equation x^2 - 16 = 0 are x = -4 and x = 4.
What is the strategy for factoring trinomial quadratic equations as shown in the video?
-The strategy for factoring trinomial quadratic equations is to find two numbers that multiply to the constant term and add up to the coefficient of the linear term.
For the equation x^2 - 7x + 12 = 0, what factors are chosen and why?
-For the equation x^2 - 7x + 12 = 0, the factors chosen are (x - 4) and (x - 3) because their product is -12 and their sum is -7.
What are the solutions for the equation x^2 - 7x + 12 = 0?
-The solutions for the equation x^2 - 7x + 12 = 0 are x = 4 and x = 3.
Outlines

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードMindmap

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードKeywords

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードHighlights

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードTranscripts

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレード関連動画をさらに表示

SOLVING QUADRATIC EQUATIONS USING QUADRATIC FORMULA | Grade 9 Learning Task 3 Week 1

MATH 9 - Solving Equations Transformable to Quadratic Equation Including Rational Algebraic Equation

Math8 1G LV4 - Completing the Square and Quadratic Formula

How to Solve Quadratic Equations by Extracting the Square Root? @MathTeacherGon
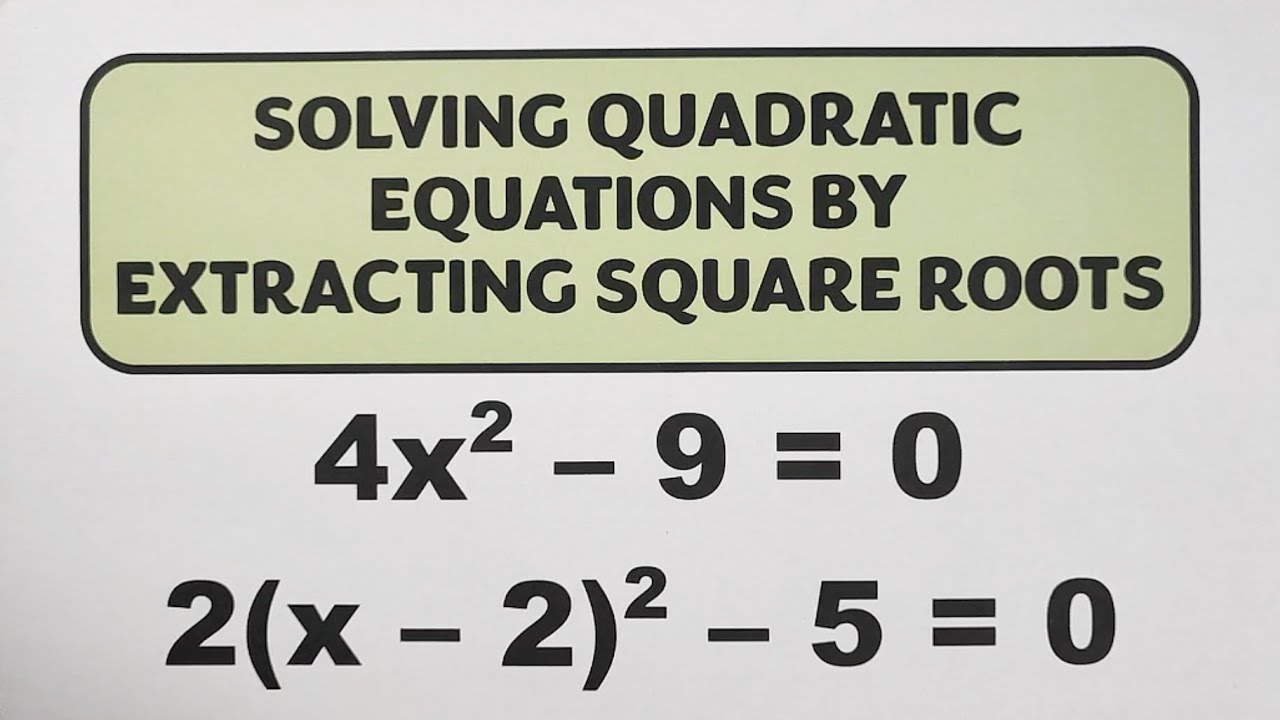
Solving Quadratic Equations by Extracting the Square Roots by @MathTeacherGon

Solving Equations Transformable into Quadratic Equations
5.0 / 5 (0 votes)
