Tipos de funciones
Summary
TLDREl guión ofrece una introducción a los tipos de funciones matemáticas, clasificándolas en dos grandes grupos: algebraicas y trascendentes. Las funciones algebraicas se subdividen en polinomiales, racionales e irracionales, mientras que las trascendentes incluyen exponenciales, logarítmicas y trigonométricas. Se describen brevemente las características de cada tipo, como las sumas y restas en polinomios, la división en racionales y las raíces en irracionales. Las trascendentes se caracterizan por variables en exponentes, logaritmos y funciones trigonométricas. El guión invita a los espectadores a aprender y identificar estas funciones, mencionando que todas pueden ser derivadas y ofrece fórmulas para ello.
Takeaways
- 📚 Las funciones matemáticas se clasifican en dos grandes grupos: algebraicas y trascendentes.
- 🔢 Las funciones algebraicas se subdividen en polinomios, racionales e irracionales.
- 📐 Los polinomios son expresiones algebraicas que pueden ser monomios, binomios, trinomios o cualquier combinación de términos.
- 📉 Las funciones racionales son cocientes de dos polinomios y representan una división.
- 🛑 Las funciones irracionales incluyen expresiones con raíces, como la raíz cuadrada o cúbica.
- 📈 Las funciones trascendentes se dividen en exponenciales, logarítmicas y trigonométricas.
- 🔢 Las funciones exponenciales tienen la variable en el exponente, como en 'e^x' o '2^(x+1)'.
- 📊 Las funciones logarítmicas representan el inverso de la exponenciación, con logaritmos naturales o base 10.
- 📐 Las funciones trigonométricas utilizan funciones como el seno, la coseno y la tangente aplicadas a variables.
- 📝 Cada tipo de función tiene características únicas y fórmulas de derivación específicas.
- 👨🏫 El análisis y aprendizaje de estas funciones es fundamental para comprender el álgebra y la cálculo.
Q & A
¿Cuántos tipos de funciones se mencionan en el guión y cómo se clasifican?
-Se mencionan dos tipos de funciones: algebraicas y trascendentes. Las funciones algebraicas se dividen en polinomios, racionales e irracionales, mientras que las trascendentes se dividen en exponenciales, logarítmicas y trigonométricas.
¿Qué es un polinomio y cómo se forman?
-Un polinomio es una función algebraica formada por una cadena de sumas y restas de potencias enteras de la variable. Puede estar formada por un monomio, binomio, trinomio o cualquier expresión algebraica.
¿Cómo se define una función racional y cómo se identifica?
-Una función racional se define como el cociente de dos funciones polinomiales. Se identifica cuando vemos una expresión en la que una polinomio está dividida por otro polinomio.
¿Qué características tienen las funciones irracionales?
-Las funciones irracionales incluyen expresiones radicales, como por ejemplo, una raíz cuadrada de una expresión algebraica que contiene la variable.
¿Qué son las funciones exponenciales y cómo se identifican?
-Las funciones exponenciales son aquellas que constan de una base numérica y una expresión variable como exponente. Se identifican cuando la variable aparece en la posición del exponente.
¿Cómo se definen las funciones logarítmicas y cuáles son sus tipos?
-Las funciones logarítmicas se definen como el logaritmo de una expresión variable. Pueden ser logaritmos naturales o base 10, y se identifican por la presencia de un logaritmo en la función.
¿Qué son las funciones trigonométricas y qué características tienen?
-Las funciones trigonométricas son aquellas que contienen funciones trigonométricas como seno, coseno, tangente, secante, etc., aplicadas a una cantidad variable. Se caracterizan por la utilización de estas funciones trigonométricas.
¿Cómo se puede identificar una función algebraica en comparación con una trascendente?
-Una función algebraica es cualquier expresión algebraica que no involucra funciones exponenciales, logarítmicas o trigonométricas. Mientras que las funciones trascendentes incluyen estas últimas y no son polinomios, racionales o irracionales.
¿Por qué es importante la identificación de los tipos de funciones en matemáticas?
-La identificación de los tipos de funciones es importante porque cada tipo tiene propiedades y fórmulas de derivación específicas que son fundamentales para resolver problemas matemáticos y aplicarlas en diversas áreas.
¿Cómo se relacionan las funciones algebraicas y trascendentes con el proceso de derivación?
-Cada tipo de función, ya sea algebraica o trascendente, tiene su propia fórmula de derivación. Conocer a qué grupo pertenece una función ayuda a aplicar la fórmula correcta para encontrar su derivada.
¿Qué tipo de funciones se pueden derivar y por qué es esto posible?
-Todas las funciones se pueden derivar, ya que para cada tipo de función, algebraica o trascendente, existen fórmulas de derivación que permiten calcular su derivada. Esto es posible gracias a las propiedades matemáticas de cada tipo de función.
Outlines

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードMindmap

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードKeywords

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードHighlights

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレードTranscripts

このセクションは有料ユーザー限定です。 アクセスするには、アップグレードをお願いします。
今すぐアップグレード関連動画をさらに表示

Tipos de funciones matemáticas

Aprende la clasificación de las funciones matemáticas en menos de 5 minutos

Tipos de CAMISETAS SIN MANGAS para HOMBRE

Figuras literarias o retóricas

Sistema muscular: Tipos, Clasificación, Músculos principales - Anatomía Humana | Kenhub
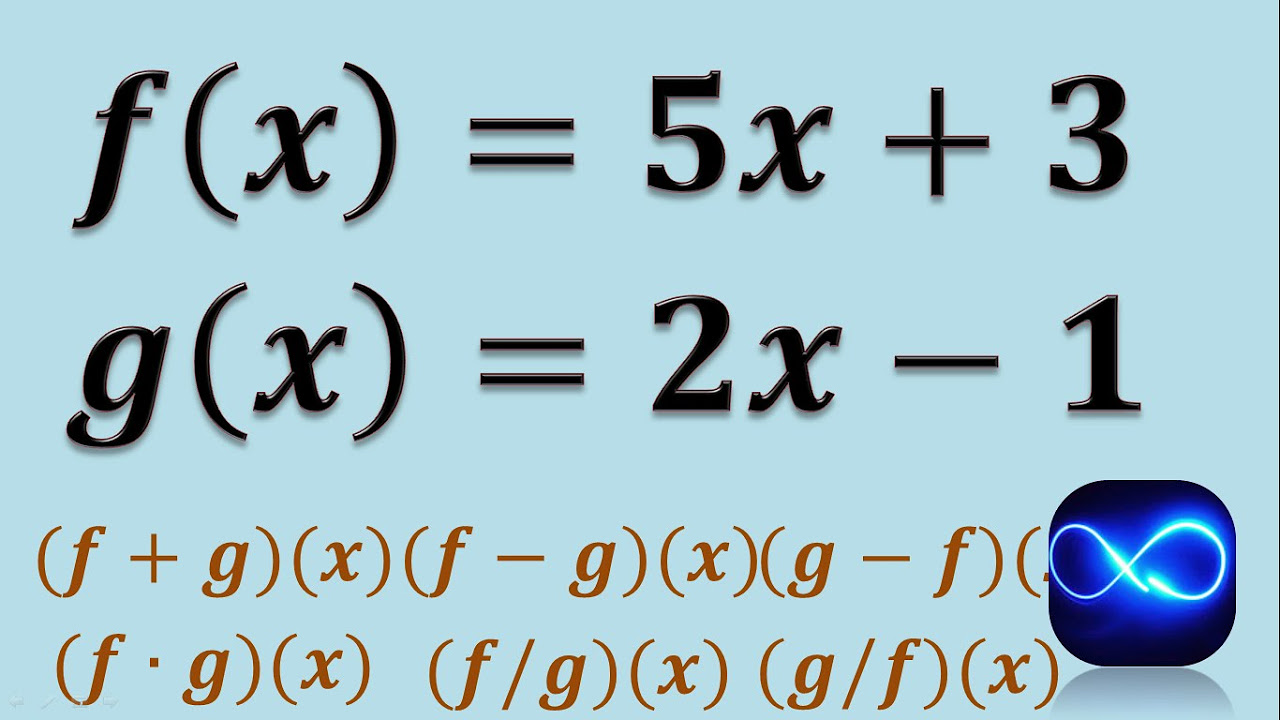
Operaciones con funciones (Suma, resta, multiplicación y división) (Ejemplo 1)
5.0 / 5 (0 votes)
