Representación de Funciones
Summary
TLDREste video enseña cómo representar funciones de cuatro maneras diferentes: mediante una tabla de tabulación, un diagrama de Venn, un conjunto de pares ordenados y gráficamente. Se ilustra con ejemplos cómo rellenar las tablas para después graficar o listar las parejas de valores que cumplen la fórmula dada. Aprende a identificar relaciones y a visualizarlas tanto en forma de líneas rectas como de parábolas, preparándote para entender y graficar diferentes tipos de funciones.
Takeaways
- 📚 Este es un curso sobre funciones matemáticas que enseña cómo representarlas de diferentes maneras.
- 🔍 Antes de comenzar, se recomienda entender qué es una función, tal como se explicó en un video anterior.
- 📈 Hay cuatro formas principales de representar una función: tabla de tabulación, diagrama de Venn, conjunto de pares ordenados y gráficamente.
- 📝 La tabla de tabulación es una herramienta útil para visualizar la relación entre variables y se construye con filas y columnas.
- 📉 Para construir una tabla, se deben elegir valores para la variable independiente (x) y calcular los correspondientes valores de la variable dependiente.
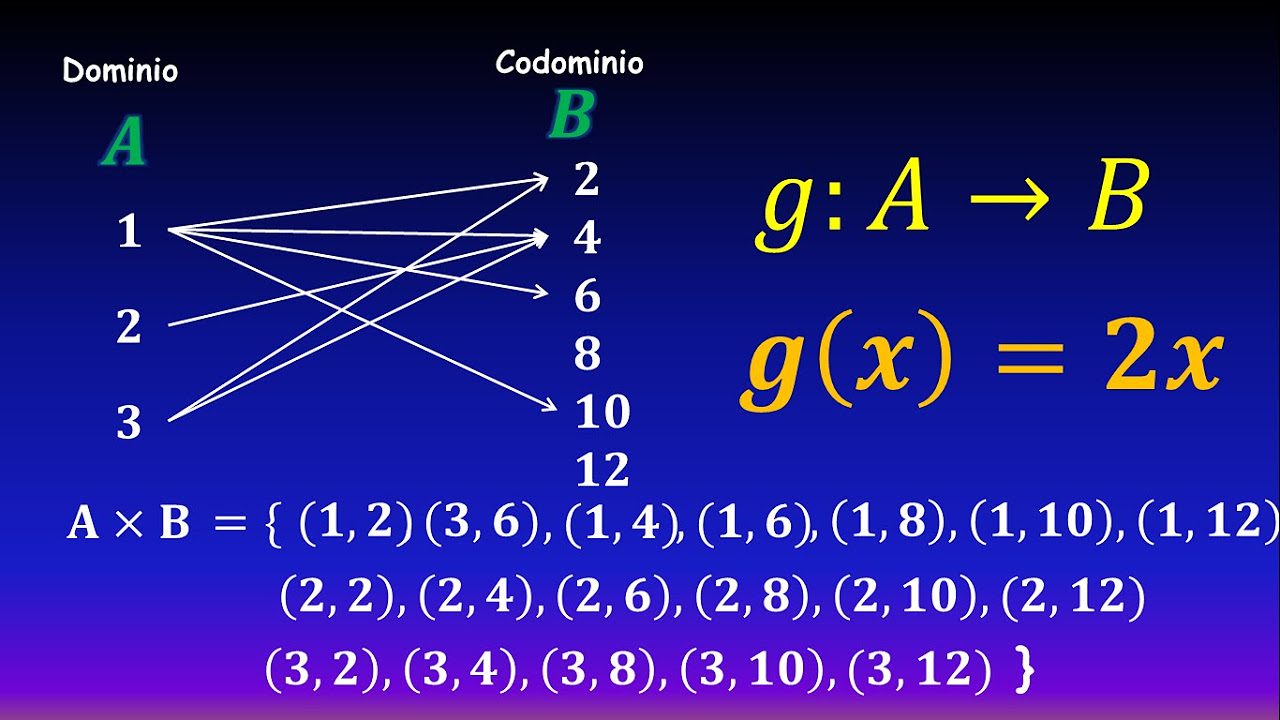
- 📊 El diagrama de Venn se utiliza para representar visualmente las relaciones entre conjuntos y se basa en las tablas de tabulación previas.
- 🔢 El conjunto de pares ordenados es una representación matemática que muestra las relaciones entre los elementos del conjunto de salida y de llegada.
- 📈 La gráfica es una representación visual de una función que permite ver cómo varía una variable en relación a otra.
- 📐 Al graficar, es importante entender que diferentes funciones tienen formas distintas, como líneas rectas o parábolas.
- 👨🏫 El video ofrece ejemplos prácticos para ilustrar cómo se construyen las tablas y cómo se grafican las funciones.
- 🚀 Se invita a los espectadores a dejar comentarios, dar like, compartir y seguir aprendiendo sobre funciones en los próximos videos.
Q & A
¿Cuántas formas de representar una función se mencionan en el script del video?
-Se mencionan cuatro formas de representar una función: la tabla de tabulación, el diagrama de Venn, el conjunto de pares ordenados y la representación gráfica.
¿Qué es la variable independiente y cómo se representa en una tabla de tabulación?
-La variable independiente es la que no depende de nada y representa los elementos del conjunto de salida. En una tabla de tabulación, se coloca en la primera columna y se utiliza para determinar los valores de la variable dependiente.
¿Cómo se calcula el valor de una función en una tabla de tabulación?
-Para calcular el valor de una función en una tabla de tabulación, se reemplaza el valor de la variable independiente (x) en la fórmula general de la función y se realiza la operación correspondiente para obtener el valor de la variable dependiente.
¿Qué es un diagrama de Venn y cómo se utiliza para representar funciones?
-Un diagrama de Venn es una representación visual de conjuntos y sus relaciones. Para representar funciones, se marcan los elementos relacionados en el diagrama, utilizando los valores de una tabla de tabulación previamente calculada.
¿Cómo se representa un conjunto de pares ordenados para una función?
-Un conjunto de pares ordenados se representa haciendo parejas de los elementos que se relacionan, colocándolos en paréntesis separados por una coma. En la primera componente se colocan los elementos del conjunto de salida (x) y en la segunda componente, los elementos del conjunto de llegada (f(x)).
¿Qué es la gráfica de una función y cómo se construye a partir de una tabla de tabulación?
-La gráfica de una función es una representación visual de cómo varía la variable dependiente con respecto a la variable independiente. Se construye trazando un plano, ubicando los puntos correspondientes a los pares de la tabla de tabulación y uniendo estos puntos con una línea o curva que represente la función.
¿Por qué es importante utilizar la fórmula general de una función al llenar una tabla de tabulación?
-La fórmula general de una función es importante porque nos indica cómo se relacionan los elementos de la variable independiente con la variable dependiente. Utilizarla al llenar una tabla de tabulación nos asegura de calcular correctamente los valores de la función para cada valor de x.
¿Cómo se identifican los puntos en un plano para graficar una función?
-Para identificar los puntos en un plano para graficar una función, se utilizan los valores de la variable independiente (x) y se calcula el correspondiente valor de la variable dependiente (f(x)) utilizando la fórmula general de la función. Estos valores se marcan en el plano y se conectan para formar la gráfica.
¿Cuál es la diferencia entre una línea recta y una parábola en términos de gráficas de funciones?
-Una línea recta es una gráfica que representa una función lineal donde la variable dependiente varía a una tasa constante con respecto a la variable independiente. Una parábola, por otro lado, es una gráfica que representa una función cuadrática y muestra una variación no lineal, típicamente con una forma de abanico.
¿Qué tipo de función se representa con una línea recta en el script del video?
-En el script del video, la función 'f(x) = x + 2' se representa con una línea recta en la gráfica.
¿Cómo se describe la parábola en la gráfica para la función 'f(x) = x^2 - 1' según el script del video?
-Según el script del video, la parábola para la función 'f(x) = x^2 - 1' se describe a través de puntos que no se pueden unir con una línea recta y que forman una curva que es característica de una parábola.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes

Cómo hacer diagramas de Venn-Euler | Teoria de Conjuntos

Diagrama de cajas y bigotes | Boxplot

Diagramas de Venn

Identificar a una Función o Relación de un Conjunto
01. ¿Qué es una Función? (Funciones, relaciones, producto cartesiano)

COMO INTERPRETAR los datos de una TABLA DE FRECUENCIA - EJEMPLO PRÁCTICO
5.0 / 5 (0 votes)
