FUNCIÓN CUADRÁTICA - Cómo graficarla calculando todos sus puntos mas importante
Summary
TLDREste video tutorial enseña cómo graficar una función cuadrática paso a paso, comenzando con el cálculo y la ubicación de puntos clave como el vértice, las raíces, la ordenada al origen y el eje de simetría. Se explica cómo usar las fórmulas para encontrar el vértice y las raíces, cómo identificar la intersección con el eje y y cómo trazar la parábola de manera precisa en una hoja cuadriculada. Es un recurso útil para quienes desean entender el proceso de graficado de funciones cuadráticas de forma clara y detallada.
Takeaways
- 😀 El vértice es uno de los puntos más importantes de la parábola, ya que es donde se originan las dos ramitas.
- 😀 La fórmula para calcular la coordenada x del vértice es: x = -b / (2a).
- 😀 La coordenada y del vértice se encuentra sustituyendo el valor de x en la ecuación original de la parábola.
- 😀 El coeficiente 'a' es el número que acompaña a la x², 'b' es el coeficiente de la x, y 'c' es el término independiente.
- 😀 Las raíces de la parábola se encuentran usando la fórmula cuadrática: x = (-b ± √(b² - 4ac)) / 2a.
- 😀 Si el discriminante (b² - 4ac) es negativo, la ecuación no tiene raíces reales.
- 😀 La ordenada es el valor de la parábola cuando x = 0, y es igual al término independiente 'c'.
- 😀 El eje de simetría de la parábola es una línea vertical que pasa por el vértice y tiene la ecuación x = coordenada x del vértice.
- 😀 Para graficar la parábola, es útil usar papel cuadriculado para obtener una representación precisa y ordenada.
- 😀 Al graficar, se debe asegurarse de que la parábola sea simétrica respecto al eje de simetría, y reflejar los puntos de un lado al otro para lograr una curva equilibrada.
Q & A
¿Cuál es la fórmula para calcular la coordenada x del vértice de una parábola?
-La fórmula para calcular la coordenada x del vértice es: x = -b / (2a), donde 'a' es el coeficiente de x² y 'b' es el coeficiente de x en la ecuación cuadrática.
¿Cómo se calcula la coordenada y del vértice de una parábola?
-Para calcular la coordenada y del vértice, se sustituye el valor de x obtenido en la fórmula del vértice en la ecuación cuadrática original.
¿Qué pasos debo seguir para encontrar las raíces de una parábola?
-Para encontrar las raíces, utilizamos la fórmula cuadrática: x = (-b ± √(b² - 4ac)) / 2a. Primero sustituimos los valores de a, b y c, y luego resolvemos para encontrar las dos posibles raíces.
¿Qué pasa si el discriminante (b² - 4ac) es negativo al calcular las raíces?
-Si el discriminante es negativo, significa que no existen raíces reales, ya que no se puede calcular la raíz cuadrada de un número negativo.
¿Qué es la ordenada o intersección con el eje y?
-La ordenada es el punto donde la parábola corta al eje y. Para encontrarla, se establece x = 0 en la ecuación cuadrática y se resuelve para y.
¿Por qué es importante la simetría de la parábola al graficarla?
-La simetría de la parábola es fundamental porque nos permite usar un lado de la parábola para reflejar y completar el otro lado, garantizando una gráfica precisa.
¿Qué es el eje de simetría de la parábola?
-El eje de simetría es una línea vertical que pasa por el vértice de la parábola, dividiéndola en dos partes iguales. Su ecuación es x = (valor de la coordenada x del vértice).
¿Cómo se determina la posición del vértice en el gráfico?
-El vértice se ubica en las coordenadas (x, y), donde x se calcula usando la fórmula x = -b / (2a) y y se obtiene sustituyendo x en la ecuación cuadrática original.
¿Qué ocurre si el término independiente (c) es negativo al encontrar la ordenada?
-Si el término independiente c es negativo, el valor de la ordenada será negativo, lo que significa que la parábola corta el eje y por debajo del origen.
¿Cómo puedo mejorar la precisión al graficar una parábola en papel cuadriculado?
-Para mejorar la precisión, se recomienda utilizar papel cuadriculado, marcar el eje cartesiano con precisión y usar los puntos calculados (vértice, raíces y ordenada) para trazar la parábola, aprovechando la simetría.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes

Funciones Cuadráticas (Definición, propiedades y representación)

Función cuadrática dada en forma factorizada

FUNCIÓN CUADRÁTICA: Explicación Completa y Cómo Graficarla

Función cuadrática. Gráfico: hallando vértice, raíces, ordenada al origen. Parte1/7

Funciones CUADRÁTICAS 📝 Vértice, Puntos de Corte con los ejes y Representación
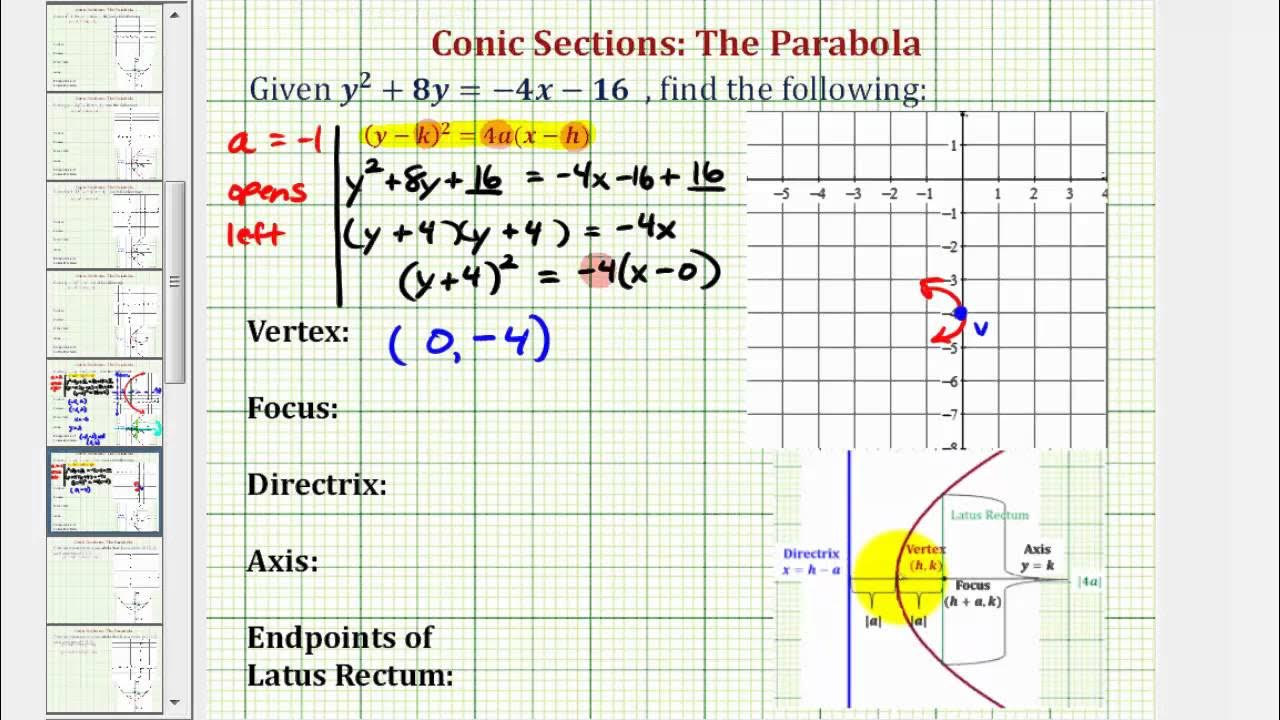
Ex 10: Conic Section: Parabola with Horizontal Axis and Requires Completing the Square (Left)
5.0 / 5 (0 votes)
