calc 3 vector fields
Summary
Please replace the link and try again.
Please replace the link and try again.
Q & A
Qu'est-ce qu'un champ vectoriel conservatif et comment le vérifier ?
-Un champ vectoriel conservatif est un champ dont le travail effectué sur un chemin fermé est nul. Pour vérifier si un champ vectoriel est conservatif, on doit examiner les dérivées partielles croisées des composants du champ. Si ces dérivées sont égales, le champ est conservatif.
Pourquoi est-il important de vérifier les dérivées partielles croisées d'un champ vectoriel ?
-Les dérivées partielles croisées permettent de déterminer si un champ vectoriel est conservatif. Si ces dérivées ne sont pas égales, cela indique que le champ n'est pas conservatif, ce qui a des implications dans des applications comme le travail d'un champ de force ou l'intégration de surfaces.
Que représentent les fonctions p, q, et r dans l'exemple ?
-Dans l'exemple, p, q et r représentent les composantes d'un champ vectoriel. P est la fonction en fonction de y, q est la fonction en fonction de x et r est une fonction qui dépend de x, y et z.
Pourquoi les dérivées partielles de p par rapport à y et de q par rapport à x étaient égales dans le premier test ?
-Les dérivées partielles de p par rapport à y et de q par rapport à x étaient égales car les termes impliqués ne contiennent que des variables qui ne changent pas de manière significative par rapport à ces variables respectives. Par conséquent, ces dérivées sont égales et montrent que la première condition pour un champ conservatif est respectée.
Pourquoi le champ vectoriel n'est-il pas conservatif après le second test de dérivées partielles ?
-Le champ vectoriel n'est pas conservatif après le second test car les dérivées partielles croisées de la fonction x par rapport à z et de la fonction z par rapport à x ne sont pas égales. Cette inégalité montre que le champ ne satisfait pas aux conditions d'un champ conservatif.
Quelle est la signification du fait que les dérivées partielles de x par rapport à z et de r par rapport à x ne soient pas égales ?
-Le fait que ces dérivées ne soient pas égales signifie que le champ vectoriel présente une dépendance non conservée entre ses composantes x et z. Cela empêche le champ d'être conservatif, car dans un champ conservatif, les dérivées croisées doivent être égales.
Que se passe-t-il si les dérivées partielles croisées d'un champ vectoriel ne sont pas égales ?
-Si les dérivées partielles croisées d'un champ vectoriel ne sont pas égales, cela indique que le champ n'est pas conservatif. Cela signifie que le travail effectué par ce champ sur un chemin fermé n'est pas nul, ce qui va à l'encontre de la définition d'un champ conservatif.
Quel est le rôle de l'examen des dérivées partielles de q et r dans l'exemple ?
-L'examen des dérivées partielles de q et r permet de vérifier une autre condition pour la conservativité du champ. Bien que cette étape ne soit pas strictement nécessaire après avoir trouvé une inégalité dans les tests précédents, elle permet de renforcer la conclusion que le champ n'est pas conservatif.
Pourquoi la dérivée partielle de x par rapport à z dans le dernier test est égale à zéro ?
-La dérivée partielle de x par rapport à z est égale à zéro parce que x est traité comme une constante par rapport à z. En d'autres termes, x ne dépend pas de z, ce qui rend sa dérivée nulle.
En quoi consiste la méthode des dérivées partielles croisées pour déterminer si un champ vectoriel est conservatif ?
-La méthode des dérivées partielles croisées consiste à calculer les dérivées partielles de chaque composante du champ vectoriel par rapport aux variables associées et à vérifier si elles sont égales. Si les dérivées croisées de toutes les composantes sont égales, le champ est conservatif. Sinon, il ne l'est pas.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes
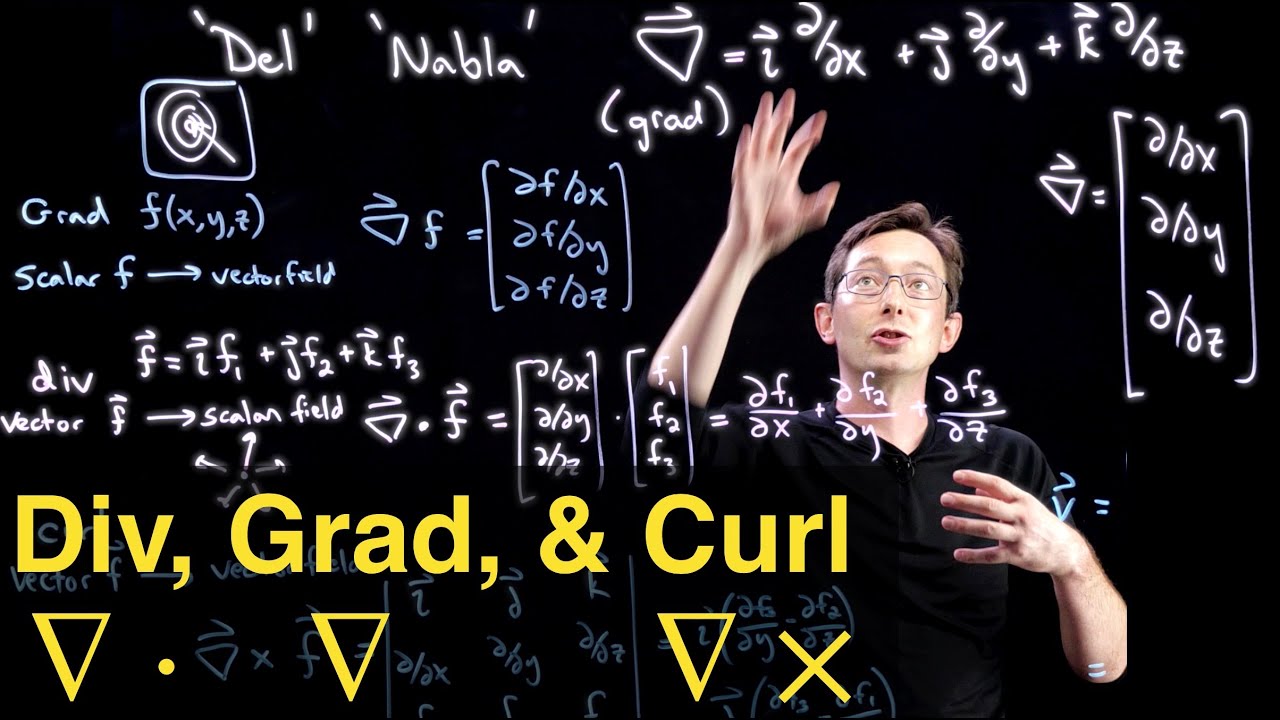
Div, Grad, and Curl: Vector Calculus Building Blocks for PDEs [Divergence, Gradient, and Curl]
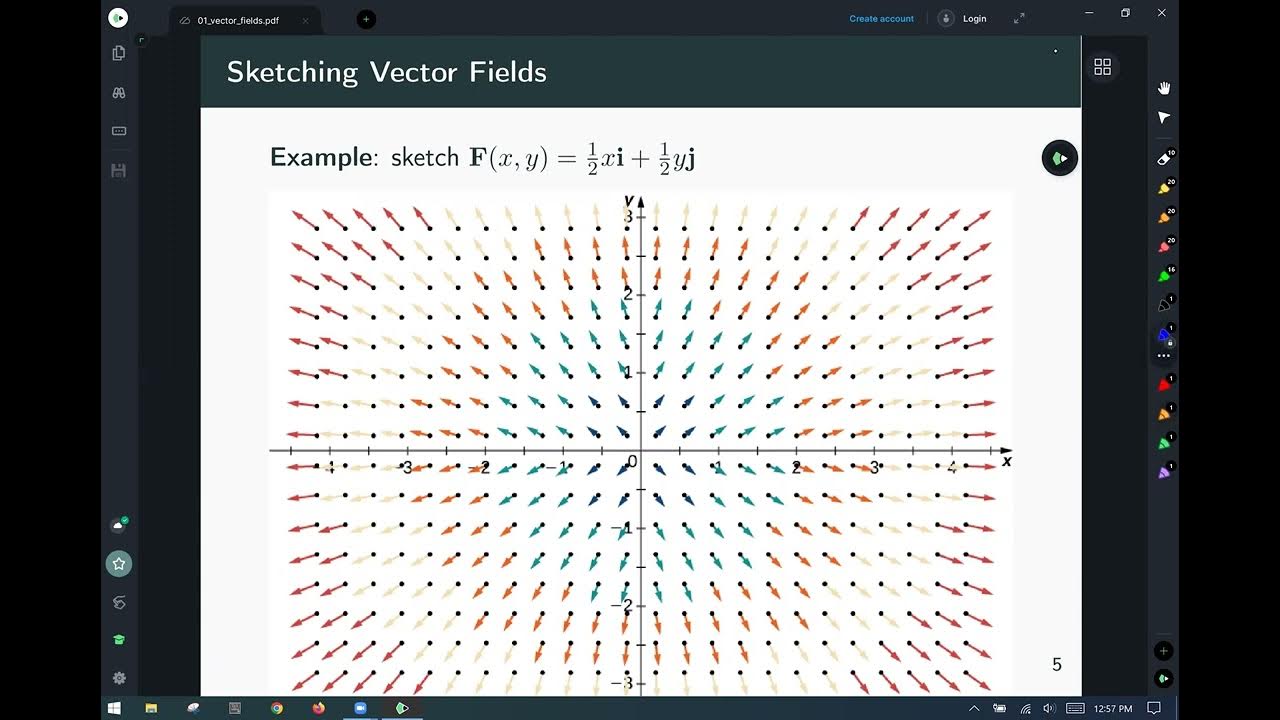
calc 3 vector fields

Tensor Calculus 4: Derivatives are Vectors

Divergence and Curl of vector field | Irrotational & Solenoidal vector

Vector Calculus Module 4 Core Ideas

2.- Aprende Excel Desde Cero - Historia de las Hojas de Calculo
5.0 / 5 (0 votes)