Hiç Kimsenin Doğru Çözemediği SORU!
Summary
TLDRThis video explores a deceptively simple problem involving two circles with different sizes rolling around each other. At first glance, the solution seems to suggest that the smaller circle should complete three rotations around the larger one. However, the real answer is four rotations due to the complexities of reference frames and circular motion. The video delves into the concept of reference frames, illustrating how our intuition can be easily misled. It also discusses the importance of being open to different perspectives and the humility to revise one's understanding, drawing a parallel to real-life lessons about skepticism and learning.
Takeaways
- 😀 The problem involves two circles, one with a radius three times larger than the other, and the task is to determine how many times the smaller circle rolls around the larger one.
- 😀 The intuitive answer to the problem is that the smaller circle will roll three times around the larger one, as it's three times smaller in size.
- 😀 However, the correct answer is four rotations, not three, which challenges our initial intuition about the problem.
- 😀 The problem was actually presented in a university entrance exam in the US in 1982, and many students initially got the wrong answer.
- 😀 The real difficulty in solving this problem lies in understanding the concept of reference frames, which greatly impacts how we interpret rotational motion.
- 😀 Reference frames are crucial in physics, as different observers may see the same motion differently depending on their perspective.
- 😀 The analogy with the Earth's movement around the Sun and its own rotation illustrates how reference frames influence how we perceive motion over time.
- 😀 The problem is simple but has a surprising complexity because it asks us to think beyond our intuition and consider the proper frame of reference.
- 😀 The mistake people make is assuming that the smaller circle's rotations are equivalent to the ratio of the radii, but the actual physical motion requires a more nuanced approach.
- 😀 By demonstrating the rolling with physical objects, the lecturer shows that the smaller circle actually completes four rotations, which can be observed through careful observation of the reference frame.
- 😀 This example underscores the importance of being open to challenging our assumptions, especially when presented with an unexpected result in seemingly simple problems.
Q & A
What is the main concept discussed in the video?
-The video focuses on how seemingly simple problems, like the coin problem, can lead to unexpected outcomes depending on the reference frame from which they are viewed. It emphasizes the importance of understanding different perspectives in problem-solving.
What was the initial assumption about the coin problem?
-The initial assumption was that a smaller coin, with a radius one-third of a larger coin's radius, would complete exactly three rotations around the larger coin due to the difference in their circumferences.
Why is the answer to the coin problem not three rotations?
-The answer is not three because the problem involves different reference frames. While the smaller coin might appear to roll three times from its own center, from the perspective of the larger coin’s center, it actually completes four rotations.
How does the concept of reference frames apply in the coin problem?
-Reference frames determine how motion is perceived. In the coin problem, observing the motion from the center of the smaller coin versus the center of the larger coin leads to different answers about how many rotations occur.
How does the video connect the coin problem to the movement of the Earth and Sun?
-The video uses the Earth's movement around the Sun to explain how perspectives can alter our understanding. Just as the Earth completes a full rotation in 24 hours from our perspective but actually takes slightly longer due to its orbit, the coin problem also illustrates how simple-seeming motion can be misunderstood.
What is the significance of the 'extra 4 minutes' mentioned in the video?
-The 'extra 4 minutes' refer to the fact that while the Earth completes a full rotation in 24 hours, it actually takes about 24 hours and 4 minutes to return to the same position in the sky due to its orbital motion around the Sun. This difference emphasizes how reference frames influence time measurement.
How does the video explain the difference between 'solar time' and 'sidereal time'?
-The video explains that solar time is based on the Sun’s position in the sky, which is affected by Earth's orbital motion, resulting in a 24-hour day. Sidereal time, on the other hand, is based on the stars’ positions, and a day is slightly shorter, lasting 23 hours, 56 minutes, and 4 seconds.
How does the video connect the coin problem to modern technology issues like cybersecurity?
-The video uses the coin problem as a metaphor for the complexities and risks involved in simple-seeming issues, like cybersecurity. Just as understanding different perspectives is crucial in the coin problem, recognizing and addressing different angles and potential risks is essential in the digital world.
What lesson does the video aim to convey about problem-solving and confidence?
-The video conveys the importance of humility and openness in problem-solving. It highlights how confidence in our initial answers can sometimes blind us to alternate perspectives or corrections, and emphasizes that even experts can make mistakes.
What is the role of 'NordVPN' in the video, and how does it relate to the topic?
-NordVPN is introduced as a sponsor to highlight the importance of protecting ourselves online, drawing a parallel between understanding different perspectives in physics and recognizing different security threats in the digital world. It illustrates the need to adapt and use the right tools for protection.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes
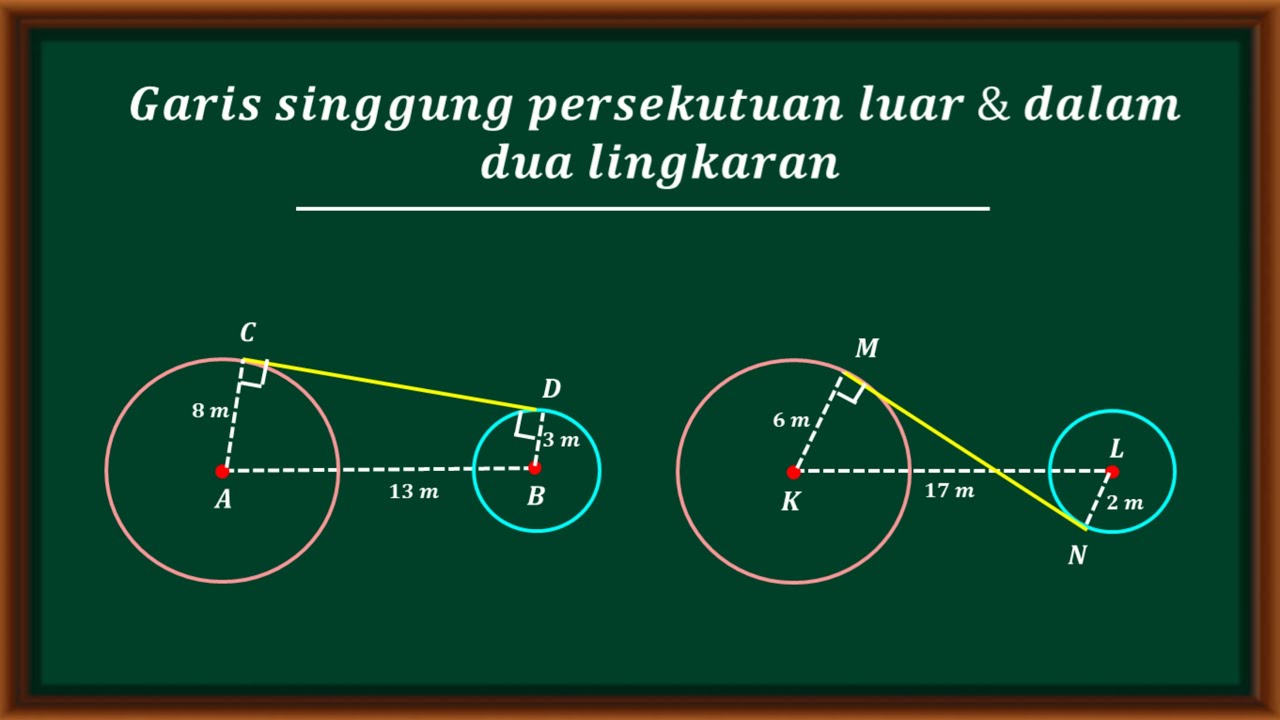
Garis singgung persekutuan luar dan garis singgung persekutuan dalam dua lingkaran

Geometry Unit 1 Lesson 4
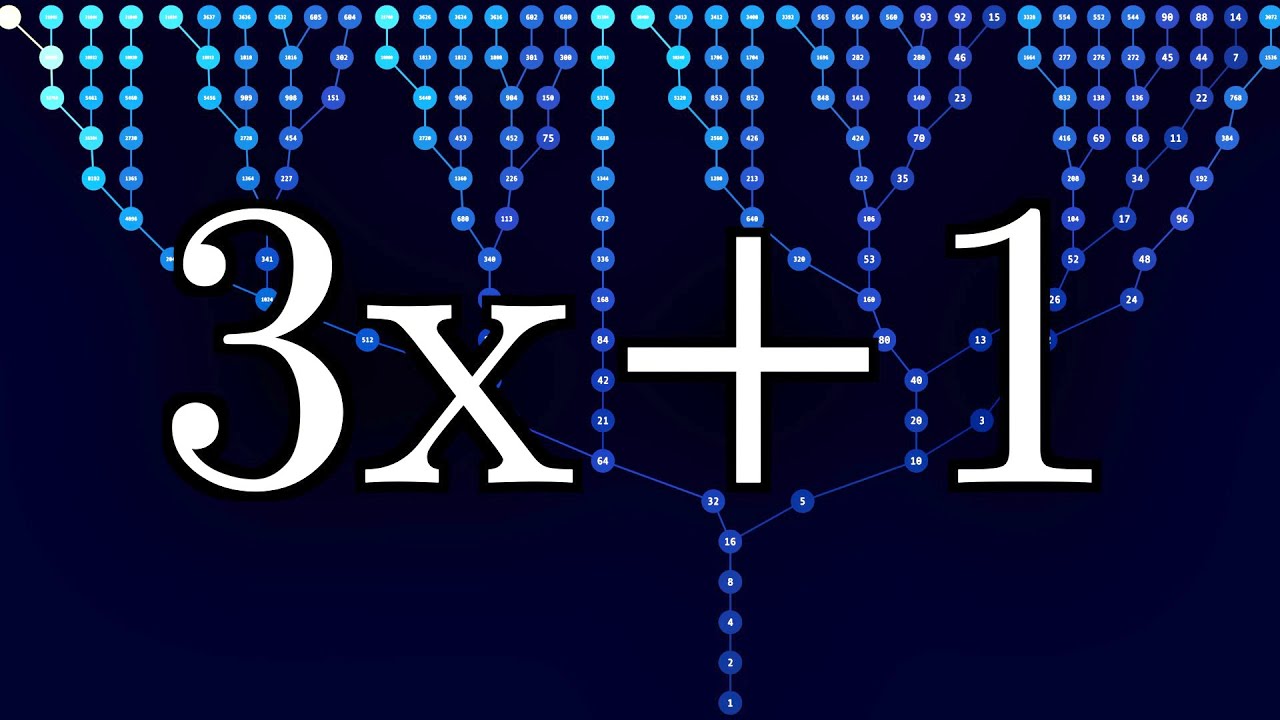
The Simplest Math Problem No One Can Solve - Collatz Conjecture

Two Dimensional Motion Problems - Physics

Lingkaran Bagian 4 - Kedudukan Dua Buah Lingkaran Matematika Peminatan Kelas XI

"Discourse." (D&D) #adnd #gundam
5.0 / 5 (0 votes)
