Metode Numerik - Metode Biseksi

Summary

In this video, the bisection method for root finding is explained in detail. Starting with two points that bracket a root, the method iteratively narrows down the interval by calculating the midpoint and evaluating the function. The segment containing the root is identified based on sign changes, allowing for continuous halving until the desired accuracy is achieved or a maximum number of iterations is reached. The video also includes practical examples to illustrate the process, making the concept accessible for learners. Overall, it provides a clear and methodical approach to solving equations numerically.

Takeaways

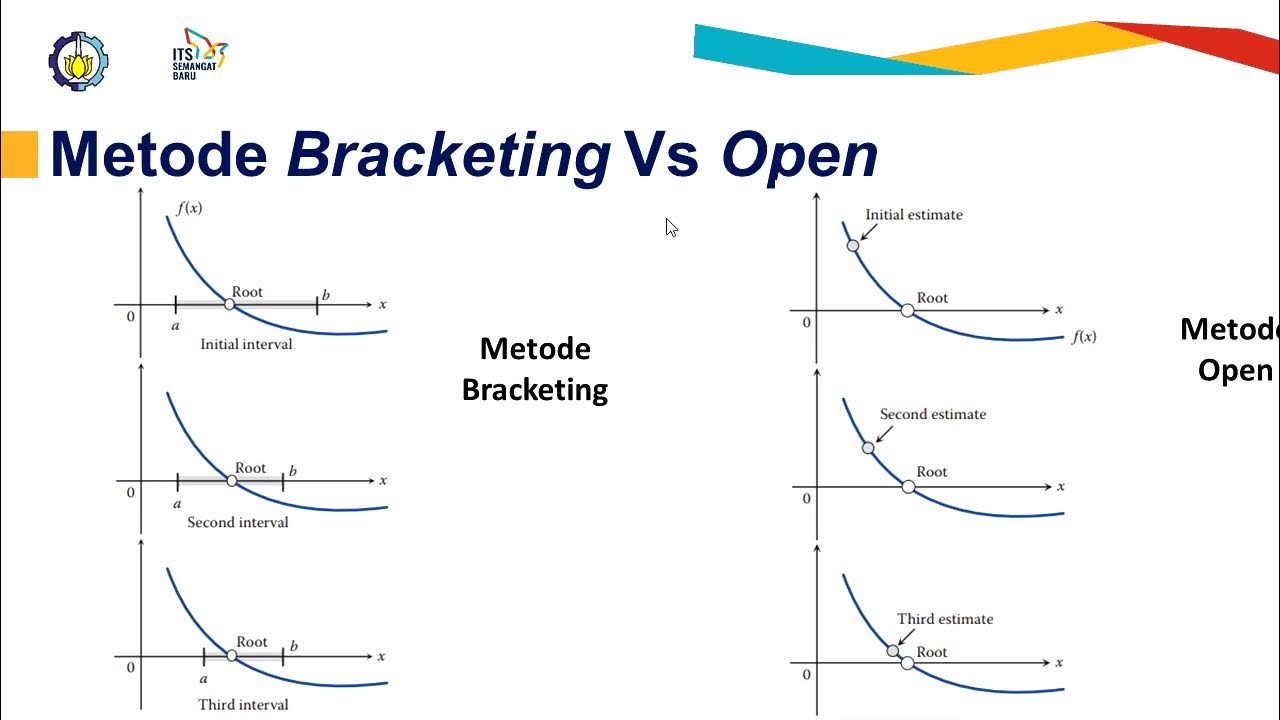
• 😀 The bisection method is a technique for finding roots of equations by dividing an interval into two parts.
• 😀 It improves upon the table method by focusing on halving the interval instead of dividing it into multiple sections.
• 😀 The initial interval [a, b] must have opposite signs for the function values at its endpoints to guarantee a root exists.
• 😀 The midpoint, c, is calculated as (a + b) / 2, and the function values at a, b, and c are compared to determine which half to eliminate.
• 😀 The process is iterative: after each iteration, the interval containing the root is halved until a desired accuracy is achieved.
• 😀 The elimination step is based on whether the function values at the endpoints and midpoint have the same sign.
• 😀 The algorithm continues until the difference between a and b is smaller than a specified error tolerance.
• 😀 The number of iterations needed increases as the desired precision decreases.
• 😀 Example calculations demonstrate how to apply the method to find a root in a specified range.
• 😀 Understanding the properties of the function and ensuring proper interval selection are crucial for the method's success.

Q & A

What is the bisection method?

The bisection method is a numerical technique used to find roots of a function by repeatedly dividing an interval in half and selecting the subinterval that contains the root.

How does the bisection method differ from the tabular method?

Unlike the tabular method, which divides the interval into multiple parts and checks all values, the bisection method only divides the interval into two halves and eliminates one half based on the signs of the function values.

What is required to apply the bisection method?

To use the bisection method, the function must have opposite signs at the endpoints of the interval, ensuring there is at least one root in that interval.

What is the significance of the midpoint in the bisection method?

The midpoint is calculated as the average of the two endpoints and is used to determine which half of the interval contains the root by comparing function values at the midpoint with those at the endpoints.

How do you determine which interval to eliminate?

You eliminate the interval that does not contain the root, based on the signs of the function values. If the midpoint shares the same sign as one endpoint, that endpoint is replaced by the midpoint.

What is meant by 'error tolerance' in this context?

Error tolerance refers to the acceptable range of error when approximating the root. The bisection method continues until the difference between the two endpoints is less than this predefined error tolerance.

What does the iteration process in the bisection method entail?

The iteration process involves repeatedly calculating the midpoint, evaluating the function at this point, and updating the interval until the root is sufficiently approximated or the maximum number of iterations is reached.

How is the root approximated using the bisection method?

The root is approximated by narrowing down the interval iteratively, where each step yields a smaller interval that still contains the root, allowing for increasingly precise estimates.

What is a potential limitation of the bisection method?

The bisection method can be slow, especially if the desired error tolerance is very small, as it may require many iterations to converge to the root.

Can the bisection method be applied to functions with multiple roots?

Yes, the bisection method can be applied to functions with multiple roots, but it will only find one root in the specified interval where the signs of the function values differ.