Intro to Z-scores
Summary
TLDRThis video introduces the concept of Z-scores, focusing on their importance in statistics, particularly with normal, quantitative data. It explains how Z-scores are calculated using the mean and standard deviation, and how they help compare individual data points to the group average. The presenter uses examples like IQ scores to demonstrate Z-score calculation and interpretation, emphasizing how Z-scores indicate whether a value is above or below the mean, and how they help identify typical or unusual data points. The video provides a foundational understanding for further discussions on Z-scores.
Takeaways
- 📊 Z-scores are crucial for normal quantitative data and are used in various statistical scenarios like critical values, confidence intervals, and test statistics for proportions.
- 📉 Z-scores are based on normal distribution, where the mean and standard deviation accurately represent the data. The data must be normally distributed for the Z-score to be valid.
- 📏 The formula for calculating a Z-score involves taking the data value, subtracting the mean, and dividing by the standard deviation.
- 👍 A positive Z-score indicates a value above the mean, while a negative Z-score means the value is below the mean.
- 🧠 Example: In an IQ test with a mean of 100 and a standard deviation of 15, Maria’s IQ of 147 has a Z-score of 3.13, meaning her score is 3.13 standard deviations above the mean.
- 📐 Z-scores can be used to identify outliers, where values two standard deviations above or below the mean (Z-scores greater than or equal to 2 or less than or equal to -2) are considered unusual.
- 👥 Z-scores between -1 and 1 are typical, as they represent data that falls within one standard deviation of the mean, covering around 68% of normally distributed data.
- 🧮 Z-scores are not percentages, proportions, or units like dollars or miles. They are measured in terms of standard deviations, a way to standardize and compare data across different scales.
- 🔍 Z-scores also help in determining statistical significance, where Z-scores beyond certain thresholds indicate significantly high or low data points.
- 📚 The script emphasizes the importance of understanding Z-scores as a tool for comparing data and identifying whether data points are typical, unusual, or outliers.
Q & A
What is a z-score?
-A z-score represents the number of standard deviations a data point is from the mean. It is used to compare an individual data point to the overall dataset.
When should z-scores be used?
-Z-scores should be used when working with normal or bell-shaped data, as the calculation relies on accurate mean and standard deviation values.
How do you calculate a z-score?
-To calculate a z-score, subtract the mean from the data value, then divide the result by the standard deviation. The formula is: (data value - mean) / standard deviation.
What does a positive z-score indicate?
-A positive z-score indicates that the data value is above the mean.
What does a negative z-score indicate?
-A negative z-score indicates that the data value is below the mean.
How do you interpret z-scores in terms of outliers?
-A z-score greater than or equal to 2 indicates a high outlier, while a z-score less than or equal to -2 indicates a low outlier.
What is considered a typical z-score range?
-A typical z-score falls between -1 and 1, which corresponds to the middle 68% of values in a normal distribution.
How would you calculate the z-score for Maria's IQ of 147 if the mean is 100 and the standard deviation is 15?
-To calculate Maria's z-score, subtract 100 from 147 to get 47, then divide 47 by 15. The result is a z-score of 3.13, indicating that Maria's IQ is 3.13 standard deviations above the mean.
What does a z-score of 3.13 for Maria’s IQ mean?
-Maria’s z-score of 3.13 means her IQ is 3.13 standard deviations above the mean, indicating that she has an unusually high IQ compared to the general population.
How do z-scores relate to significance in statistics?
-Z-scores are often used in significance testing. Values greater than or equal to 2 (or less than or equal to -2) are considered unusual and may indicate statistical significance.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes
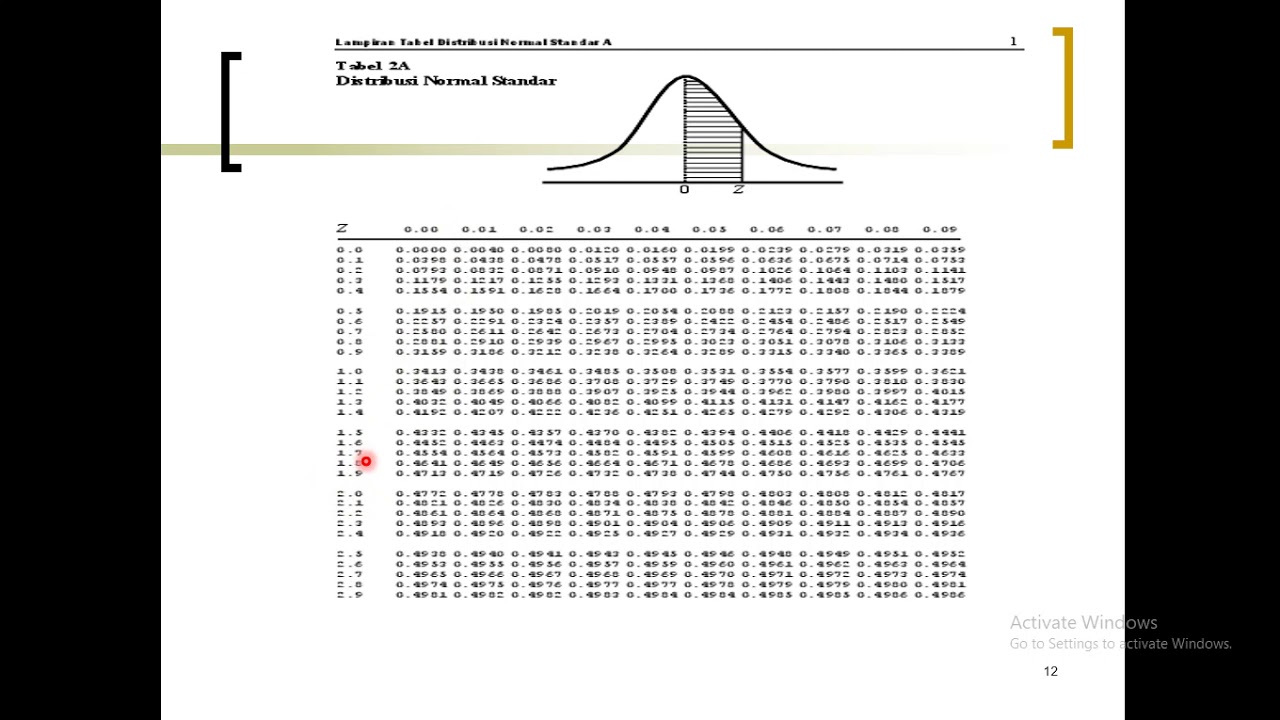
Distribusi Probabilitas Normal

Statistika Matematika Kelas 12 • Part 1: Pengertian Statistika dan Jenis-Jenis Data
Distribusi Normal | Konsep Dasar dan Sifat Kurva Normal | Matematika Peminatan Kelas 12

CONVERTING A NORMAL RANDOM VARIABLE TO A STANDARD NORMAL VARIABLE AND VICE VERSA

Z-Scores and Percentiles: Crash Course Statistics #18

[PART 1] STATISTIKA PENDIDIKAN: MENGENAL DATA
5.0 / 5 (0 votes)
