79. OCR A Level (H046-H446) SLR13 - 1.4 Floating point binary part 1 - Overview
Summary
TLDRThis video is the first in a series explaining floating point binary representation. It begins with an 8-bit binary number line, illustrating how integers and fractions are represented. The video then transitions to fixed point binary, where the binary point's position is fixed, limiting the range of numbers that can be stored. To overcome this, floating point binary is introduced, where the binary point 'floats', allowing for a trade-off between the size and accuracy of numbers. The video explains the division of bits into the mantissa (value) and exponent (binary point position), crucial for storing real numbers in binary. Examples are provided to demonstrate how numbers are converted from floating point binary to decimal.
Takeaways
- 📏 In floating point binary, the position of the binary point can change, allowing for the representation of both large and small numbers with varying degrees of precision.
- 🔢 The binary number line's place values double as you move from right to left, which is different from unsigned binary or two's complement.
- 👉 The most significant bit (leftmost bit) in floating point binary represents whether a number is negative or positive.
- 📉 To represent fractions, the number line is extended to the right, with place values halving as you move from left to right.
- 🚫 Fixed point binary has a limited range of numbers it can store accurately, as some bits are used for the fractional part of the number.
- 🔄 The method of changing the position of the binary point to increase accuracy or range is known as floating point binary.
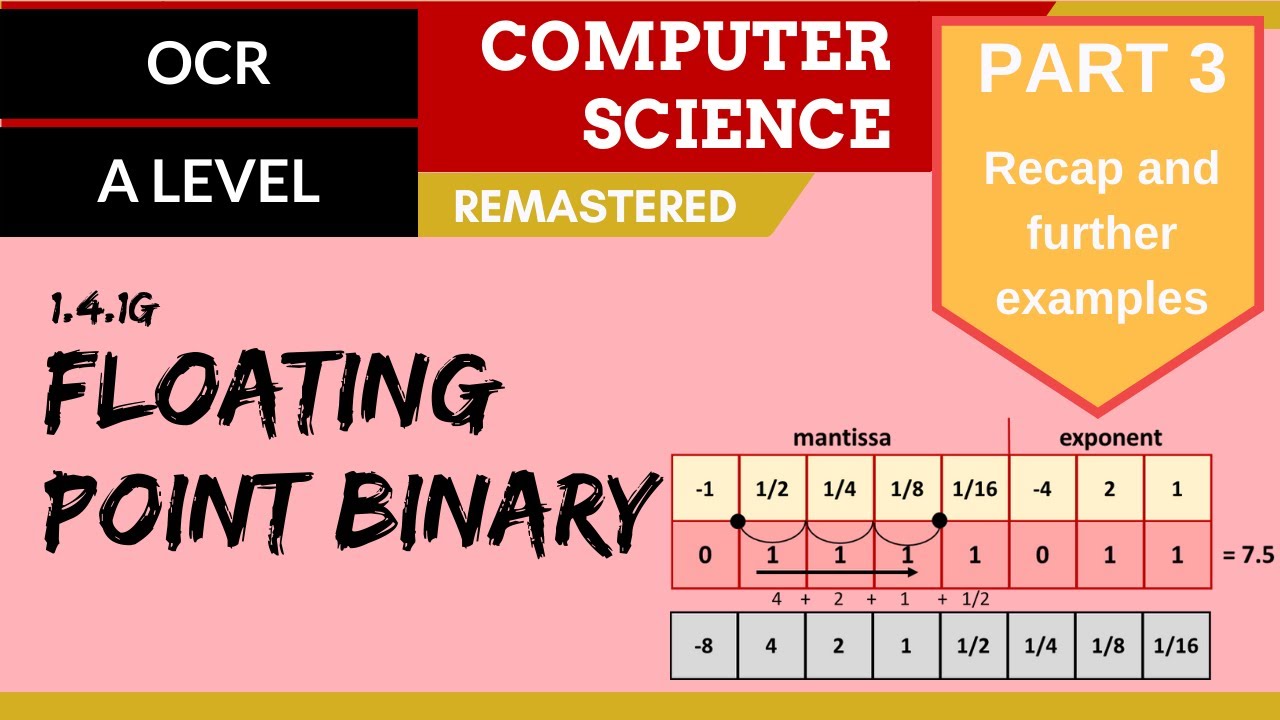
- 💾 Storing a number in floating point binary requires splitting the bits into the mantissa (the actual value) and the exponent (the position of the binary point).
- 📉 The number of bits used for the mantissa and exponent is determined by the data type, such as 24 bits for the mantissa and 8 for the exponent in a 32-bit single precision number.
- ➕ The exponent in floating point binary is stored in two's complement, which indicates how many places to move the binary point.
- 🔄 Moving the binary point to the right increases the size of the number, while moving it to the left decreases the size but can increase precision.
Q & A
What is the significance of the most significant bit in an 8-bit binary number representing a negative number?
-In an 8-bit binary number representing a negative number, the most significant bit, which is the leftmost bit, must be a 1. This bit indicates that the number is negative.
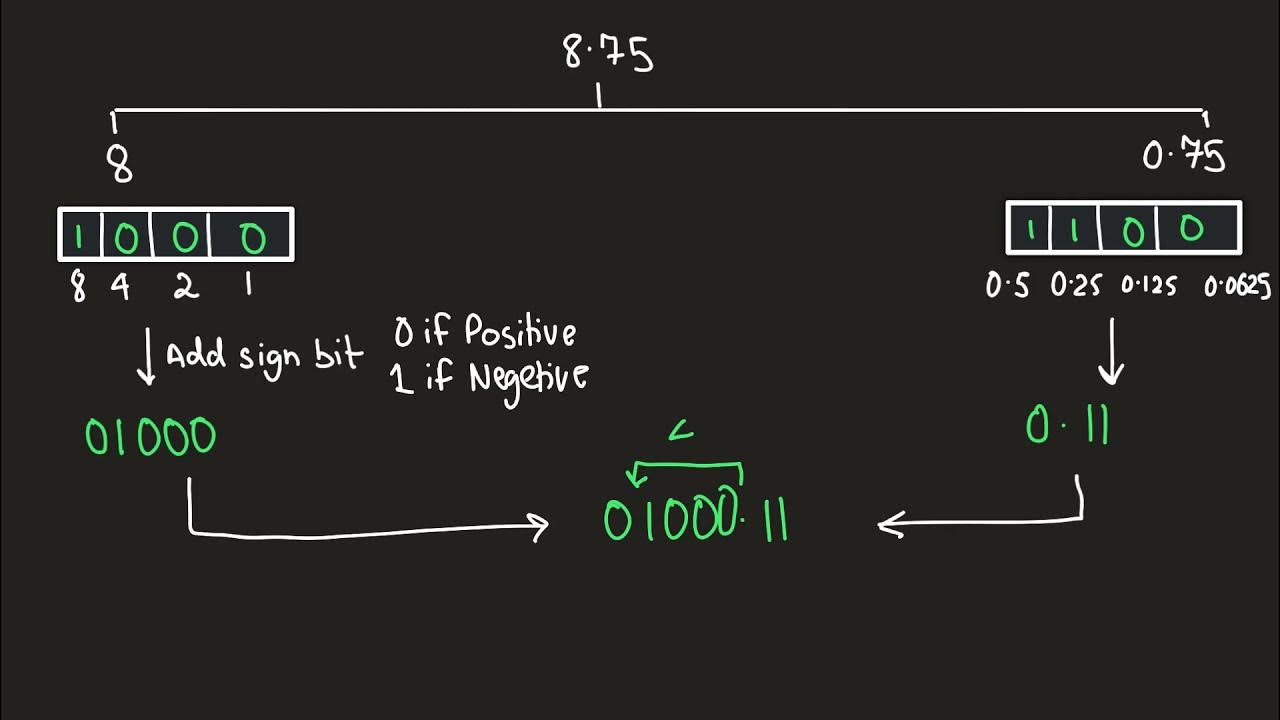
How is the number 6.5 represented in fixed point binary format?
-The number 6.5 is represented in fixed point binary format as 0011 0100. This representation includes a one in the four and two column (which equals six), plus a one in the half column, resulting in 6.5.
What is the largest positive number that can be stored in an 8-bit format using fixed point binary?
-The largest positive number that can be stored in an 8-bit format using fixed point binary is 01111111, which equals 15.875 when calculated as 8 + 4 + 2 + 1 + 0.5 + 0.25 + 0.125.
Why can't the fraction 'a third' be accurately stored in the given fixed point binary format?
-The fraction 'a third' cannot be accurately stored in the given fixed point binary format because the binary representation of a third (0.333...) would repeat infinitely, and the format does not allow for infinite precision.
How does the floating point binary system allow for a trade-off between the size and accuracy of numbers?
-The floating point binary system allows for a trade-off between the size and accuracy of numbers by adjusting the position of the binary point. More bits can be allocated to the fractional part for higher accuracy, or to the whole number part for a larger range of values.
What are the two parts that the bits in a floating point binary number are split into, and what do they represent?
-The bits in a floating point binary number are split into two parts: the mantissa, which represents the actual value of the number, and the exponent, which represents the position of the binary point within the number.
How many bits are used for the mantissa and exponent in a 32-bit single precision floating point number?
-In a 32-bit single precision floating point number, 24 bits are used for the mantissa and 8 bits for the exponent.
What does the exponent in a floating point binary number indicate?
-The exponent in a floating point binary number indicates how many places to move the binary point within the mantissa to determine the actual value of the number.
How is the position of the binary point determined in a floating point binary number?
-The position of the binary point in a floating point binary number is determined by the exponent. The binary point starts after the most significant bit in the mantissa and is moved to the right or left based on the value of the exponent.
What is the significance of backfilling zeros in the mantissa of a floating point binary number?
-Backfilling zeros in the mantissa of a floating point binary number is significant because it allows for the adjustment of the binary point's position without changing the value of the number. It is permissible as numerically, zeros are not significant.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes
81. OCR A Level (H446) SLR13 - 1.4 Floating point binary part 3 - Recap and further examples

80. OCR A Level (H046-H446) SLR13 - 1.4 Floating point binary part 2 - Normalisation

AS & A Level Computer Science (9618) - Chapter 16: ADVANCED Data Representation

Системи числення
Data Representation - Mantissa And Exponents Part 3 - (A Level Computer Science Made Easy (A2) )

HOW TO: Convert Decimal to IEEE-754 Single-Precision Binary
5.0 / 5 (0 votes)
