GEO.1.6
Summary
TLDRThe video explains various angle relationships, including vertical, adjacent, complementary, and supplementary angles. It covers how to identify these angles using examples and visual aids, emphasizing key concepts like congruence and linear pairs. The instructor also provides tips on distinguishing between complementary and supplementary angles, using memorable tricks. The video concludes with exercises on solving for unknown angles using algebra, applying the angle relationships discussed. Viewers are encouraged to practice on their own and check their answers.
Takeaways
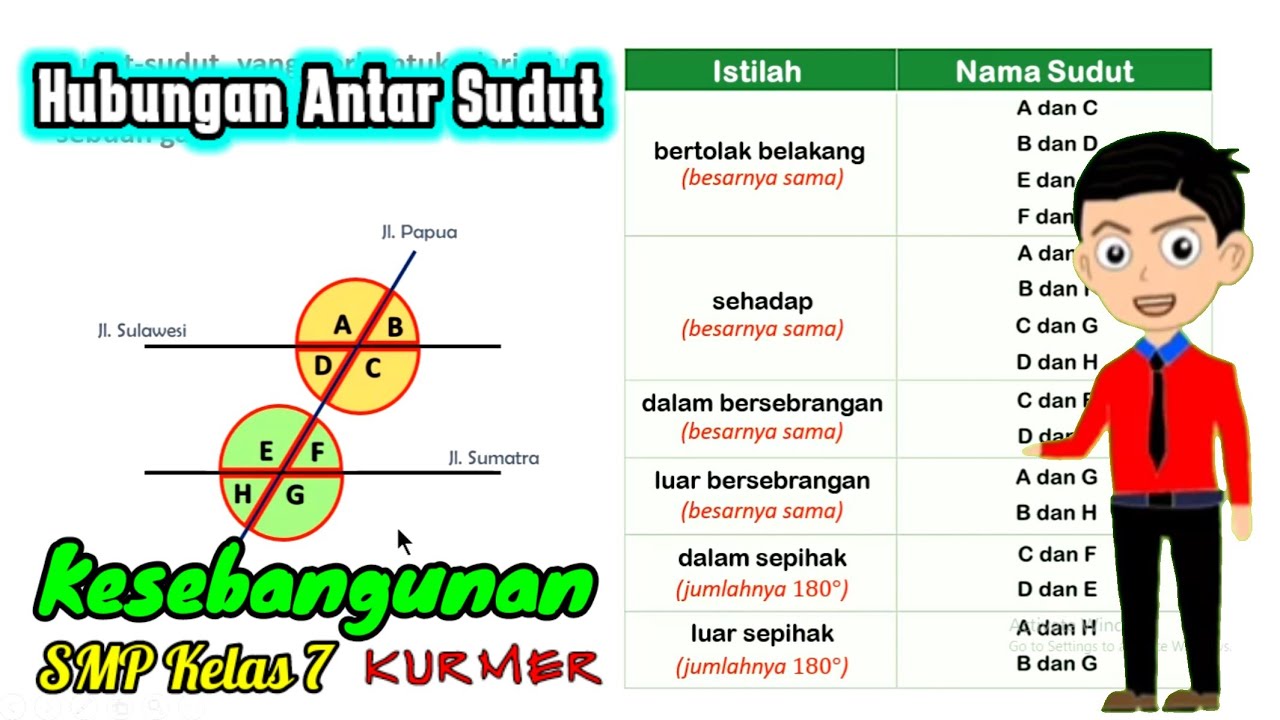
- 🔍 Vertical angles are congruent angles located across from each other on intersecting lines, like angle 1 and angle 2.
- 🎯 Adjacent angles are two angles that are next to each other and share a common side, such as angle 1 and angle 2.
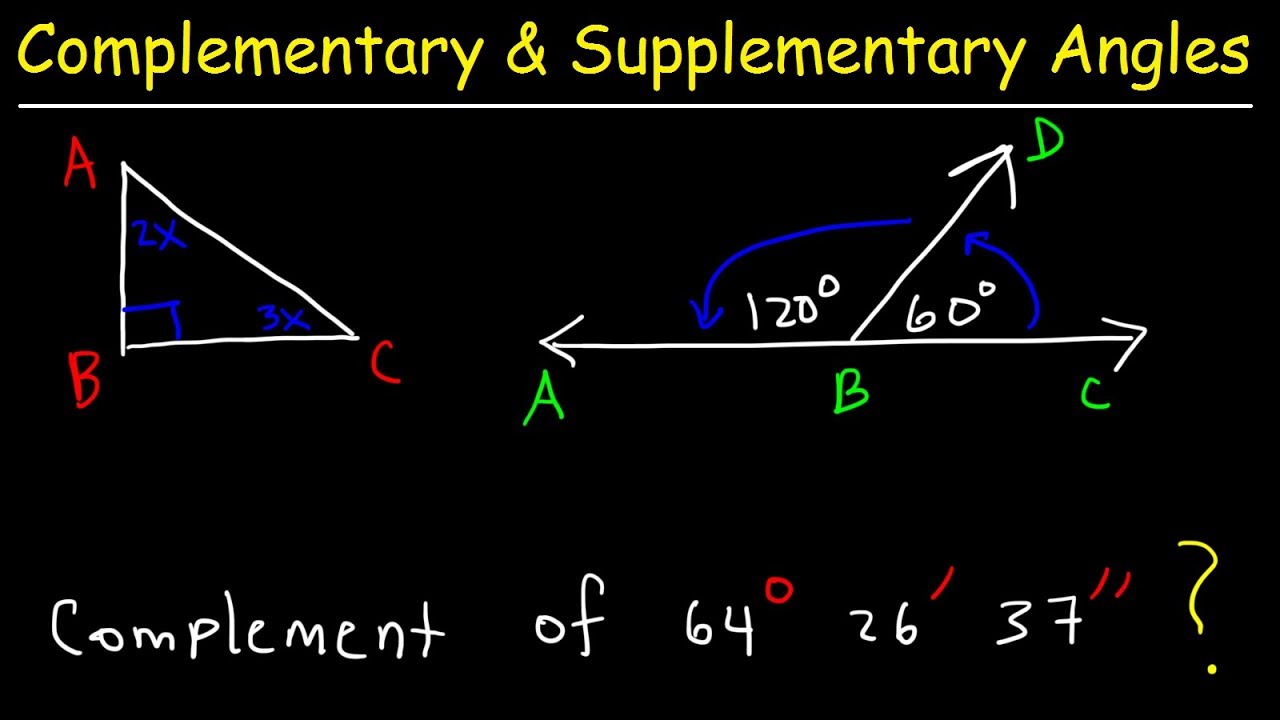
- 🎓 Complementary angles are two angles whose sum equals 90 degrees, for example, angle 1 and angle 2 summing up to 90 degrees.
- 📏 Supplementary angles are two angles whose sum is 180 degrees, like one angle being 135 degrees and another 45 degrees.
- 🔗 Linear pairs are adjacent and supplementary angles that form a straight line, with their sum always being 180 degrees.
- 📐 Vertical angles are congruent, meaning they have equal measures, like two angles each measuring 112 degrees.
- 🧮 Complementary angles add up to 90 degrees; for example, if one angle is 68 degrees, the other must be 22 degrees.
- 🔄 A linear pair is different from supplementary angles because they must be adjacent and supplementary, not just add up to 180 degrees.
- 📝 Angle relationships can be used to find unknown angle measures by applying the properties of vertical, complementary, and supplementary angles.
- 📘 For linear pairs or complementary angles, setting up equations using their properties helps in solving for unknown angles.
Q & A
What are vertical angles?
-Vertical angles are two angles that are directly across from each other on intersecting lines. They are always congruent, meaning they have the same measure.
How can you remember what vertical angles are?
-You can remember vertical angles by imagining an 'X' shape. The angles directly across from each other through the vertex are the vertical angles.
What are adjacent angles?
-Adjacent angles are two angles that are next to each other and share a common side.
What are complementary angles?
-Complementary angles are two angles whose sum is 90 degrees.
How can you distinguish between complementary and supplementary angles?
-Complementary angles sum to 90 degrees, while supplementary angles sum to 180 degrees. A helpful way to remember is that complementary angles are the 'right' thing to do (90 degrees forms a right angle).
What is a linear pair of angles?
-A linear pair consists of two adjacent angles that are supplementary. They form a straight line when combined, adding up to 180 degrees.
Do supplementary angles have to be adjacent to each other?
-No, supplementary angles do not have to be adjacent. They can be separate, but their angle measures must add up to 180 degrees.
How do you find the measure of an unknown angle using complementary angles?
-To find the measure of an unknown angle using complementary angles, subtract the measure of the known angle from 90 degrees. For example, if one angle is 68 degrees, the other would be 90 - 68 = 22 degrees.
What does it mean for angles to be bisected?
-When an angle is bisected, it is divided into two equal angles. If a line bisects an angle, the two resulting angles are congruent.
How do you solve for an unknown angle in a linear pair if given one angle's measure?
-If you know one angle in a linear pair, you can find the other by subtracting the known angle's measure from 180 degrees since the angles are supplementary. For example, if one angle is 135 degrees, the other is 180 - 135 = 45 degrees.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes
5.0 / 5 (0 votes)