DIVISIÓN DE UN SEGMENTO EN UNA RAZÓN DADA
Summary
TLDREl guion del video ofrece una introducción a la geometría analítica, específicamente sobre cómo dividir un segmento en una proporción dada. Se explica el proceso para calcular las coordenadas de un punto que divide un segmento en dos partes a una razón determinada, utilizando el sistema de coordenadas cartesiano. Además, se aplica esta teoría para encontrar el baricentro de un triángulo, trazando medianas y utilizando proporciones para calcular las coordenadas del punto que divide las medianas en partes iguales. El ejemplo práctico ilustra cómo se combinan las proporciones y las coordenadas de los vértices para hallar el baricentro, con un enfoque en la precisión y la simplificación de cálculos.
Takeaways
- 📚 La clase trata sobre la división de un segmento en una razón dada en geometría analítica.
- 📐 Se utiliza el diagrama cartesiano para representar el segmento y sus extremos con coordenadas (x1, y1) y (x2, y2).
- 🔍 Se introduce el concepto de 'punto P', que divide el segmento en dos partes y cuyo punto de división depende de una razón.
- 📈 La fórmula para calcular la abscisa del punto P se basa en la razón y las abscisas de los extremos del segmento.
- 📉 De manera similar, la ordenada del punto P se calcula a partir de la razón y las ordenadas de los extremos del segmento.
- 📝 Se enfatiza la importancia de utilizar la fórmula correcta según la razón dada (AP/PB o PB/AP).
- 📌 Se da un ejemplo práctico para ilustrar cómo calcular las coordenadas del baricentro de un triángulo, utilizando las coordenadas de sus vértices.
- 📜 El baricentro se encuentra en la intersección de las medianas de un triángulo y divide cada mediana en proporciones 2:1.
- 🔢 Se calculan las coordenadas del baricentro a través del análisis de las proporciones y las coordenadas de los vértices.
- 📐 Se describe el proceso de trazado de las medianas y cómo se determina el punto medio de un segmento para hallar el baricentro.
- 🎓 Finalmente, se resuelve un problema de ejemplo para encontrar las coordenadas del baricentro de un triángulo ABC con vértices dados.
Q & A
¿Qué tema se discute en el video sobre geometría analítica?
-El tema tratado en el video es la división de un segmento en una razón dada, cómo calcular las coordenadas de un punto que divide un segmento en dos partes proporcionalmente.
¿Qué son las coordenadas de los extremos de un segmento en un sistema de coordenadas cartesiano?
-Las coordenadas de los extremos de un segmento son dos puntos en un sistema de coordenadas cartesiano, donde cada punto tiene una abscisa (x) y una ordenada (y), representadas como (x1, y1) y (x2, y2).
¿Cómo se define el punto P en el segmento AB en el video?
-El punto P es cualquier punto ubicado en el segmento AB que divide a este segmento en dos partes, el segmento AP y el segmento PB.
¿Qué es la razón 'r' en el contexto del video?
-La razón 'r' se refiere a la proporción existente entre las medidas de los segmentos AP y PB, y es un dato conocido para calcular las coordenadas del punto P.
¿Cómo se calcula la abscisa del punto P según el video?
-Para calcular la abscisa del punto P, se toma la suma de la abscisa del punto A y el producto de la razón 'r' y la abscisa del punto B, dividido por la suma de 1 y la razón 'r'.
¿Cómo se calcula la ordenada del punto P según el procedimiento descrito en el video?
-Para calcular la ordenada del punto P, se toma la suma de la ordenada del punto A y el producto de la razón 'r' y la ordenada del punto B, dividido por la suma de 1 y la razón 'r'.
¿Qué es el baricentro de un triángulo y cómo se encuentra?
-El baricentro de un triángulo es el punto donde se intersectan las tres medianas del triángulo. Se encuentra como el punto de intersección de las medianas trazadas desde cada vértice al medio del lado opuesto.
¿Cómo se definen las medianas de un triángulo ABC según el script?
-Las medianas de un triángulo ABC son las líneas que unen cada vértice con el medio del lado opuesto, formando divisiones congruentes en los lados del triángulo.
¿Cómo se calculan las coordenadas del baricentro G de un triángulo ABC según el video?
-Para calcular las coordenadas del baricentro G, se utiliza la proporción de 2 a 1 o 1 a 2 en las medianas, y se aplican las mismas fórmulas para calcular la abscisa y la ordenada del punto P, pero con la razón correspondiente a la proporción de la mediana.
¿Cuáles son las coordenadas del baricentro del triángulo ABC en el ejemplo del video?
-Las coordenadas del baricentro del triángulo ABC en el ejemplo son (3, 3).
¿Por qué es importante conocer la razón entre los segmentos para calcular las coordenadas del punto P?
-Conocer la razón entre los segmentos es crucial para aplicar las fórmulas correctas y obtener las coordenadas precisas del punto P que divide el segmento en proporciones dadas.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados

25. Punto que divide a un segmento en una razón, EXPLICACION COMPLETA

Geometría analítica: Las rectas y sus ecuaciones

DIVISION DE UN SEGMENTO EN UN PUNTO DADO USANDO DECIMAL

Qué es una proporción EJEMPLOS

Equation of Parabola, FULL EXPLANATION

Distancia de un punto a una recta
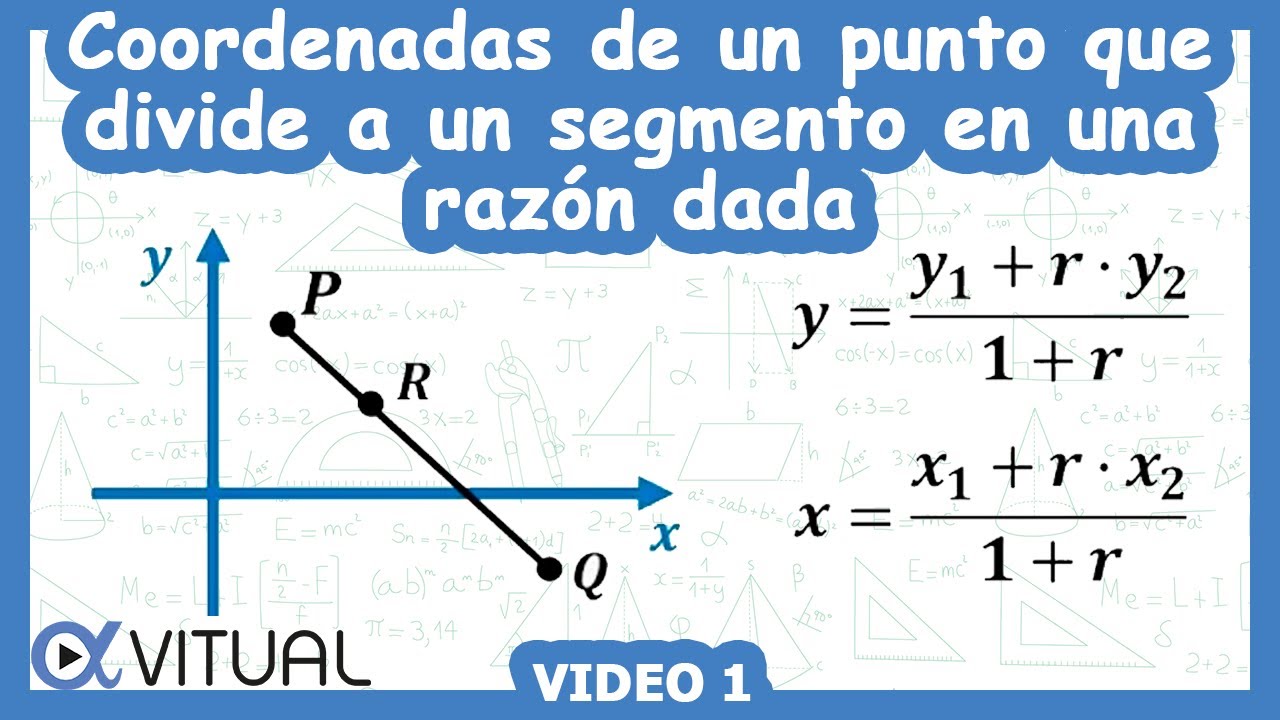
Coordenadas de un punto que divide a un segmento en una razón dada ejemplo 1 | Geometría - Vitual
5.0 / 5 (0 votes)