FIUBA. Teoría de algoritmos 1. Búsqueda Exhaustiva - Branch & Bound: Problema de la mochila

Summary

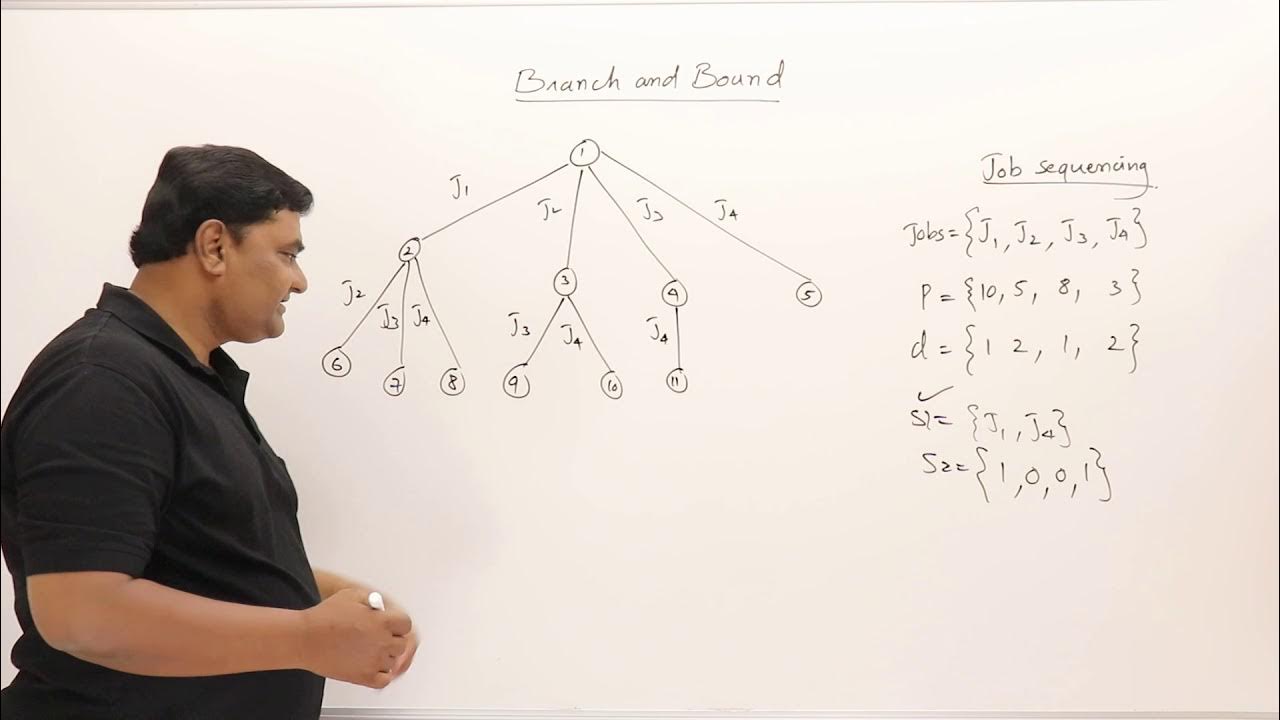
In this video, the knapsack problem is solved using the Branch and Bound method. The process involves calculating the value per unit for each item, structuring the problem into a state tree, and applying a depth-first search to explore potential solutions. The key concept is defining a cost function to estimate the maximum possible profit and pruning branches that can't yield a better solution. The method improves efficiency compared to brute force by exploring only promising solutions. The video also explains the time and space complexities involved in the algorithm, demonstrating its effectiveness for large datasets.

Takeaways

• 😀 The knapsack problem aims to select a set of elements with the highest total value, without exceeding the backpack's weight capacity.
• 😀 The Branch and Bound method solves the knapsack problem by evaluating and pruning states in a state tree to find the optimal solution.
• 😀 Each element in the knapsack has a value and a weight, and the value per unit (value/weight) is calculated to help decide which elements to prioritize.
• 😀 Elements are ordered in descending order of their value per unit to facilitate optimal decision-making during the algorithm's execution.
• 😀 The state tree is structured like a binary tree, where each node represents a decision: whether to include or exclude an element from the backpack.
• 😀 The root node represents the empty backpack, and the depth of the tree corresponds to the number of elements being considered.
• 😀 The cost function is a key concept, estimating the maximum possible profit from a given state, which helps in pruning unnecessary branches in the tree.
• 😀 The algorithm uses depth-first search (DFS) to traverse the state tree, exploring nodes based on the cost function and pruning non-promising branches.
• 😀 Pruning occurs when the cost function indicates that a branch cannot yield a better solution than the best found so far, helping reduce the search space.
• 😀 The time complexity of the Branch and Bound algorithm is O(2^n) in the worst case, where n is the number of elements in the knapsack problem.
• 😀 The space complexity is O(n), as the algorithm uses recursion and requires memory proportional to the depth of the state tree.

Q & A

What is the main objective of the knapsack problem discussed in the video?

The main objective of the knapsack problem is to select a set of elements for a backpack such that their total value is maximized without exceeding the backpack's weight capacity.

How does the Branch and Bound method help in solving the knapsack problem?

Branch and Bound helps solve the knapsack problem by systematically exploring all possible solutions using a state tree, pruning branches that cannot lead to better solutions based on a cost function.

What is the role of the value per unit in the knapsack problem?

The value per unit is used to evaluate how efficient each element is in terms of its value relative to its weight, helping to prioritize which elements to include in the knapsack for maximum profit.

Why is the state tree structure used in the Branch and Bound approach for the knapsack problem?

The state tree structure is used to represent all possible decisions (whether to include or exclude each item) in a hierarchical manner, which helps in exploring the problem efficiently and applying pruning techniques.

How is the cost function defined in the Branch and Bound approach?

The cost function is defined as the accumulated value of selected elements plus the hypothetical maximum value that could be obtained by filling the remaining space in the backpack with the next best items based on value per unit.

What does node pruning mean in the Branch and Bound method?

Node pruning refers to the process of eliminating branches in the state tree that cannot possibly lead to a better solution than the best one found so far, thereby reducing unnecessary computations.

What are the two main types of decisions at each level of the state tree?

At each level of the state tree, the two main decisions are whether to include or exclude the next element based on its value per unit and the remaining capacity of the backpack.

Why is depth-first traversal used in the Branch and Bound method?

Depth-first traversal is used because it allows for an exhaustive exploration of each possible solution path, ensuring that the best solution is found by expanding nodes and comparing their cost functions.

What happens when a node's cost function is lower than the best solution found so far?

When a node's cost function is lower than the best solution found so far, the node is pruned, meaning its descendants are not explored, as they cannot produce a better solution.

What is the time complexity of the Branch and Bound solution to the knapsack problem?

In the worst case, the time complexity is O(2^n), where n is the number of elements, because all possible combinations of elements need to be explored, although pruning can reduce this number significantly.