50s - Calculating area or circumference
Summary
TLDRThis video tutorial explains how to calculate the area and circumference of a circle, using both exact formulas and estimated values. It covers key concepts like the radius, diameter, and the mathematical constant pi (π), which is used in the formulas for circumference (π × diameter) and area (π × radius²). The video also provides examples of calculating these values, rounding for estimation, and applying them to real-world scenarios, such as fencing a circular paddock or determining the area of a path around a pond. Tips on sensible rounding and proper unit usage are also included.
Takeaways
- 😀 The radius is the distance from the center of the circle to any point on its circumference.
- 😀 The diameter is the distance across the circle through its center, and it is twice the length of the radius.
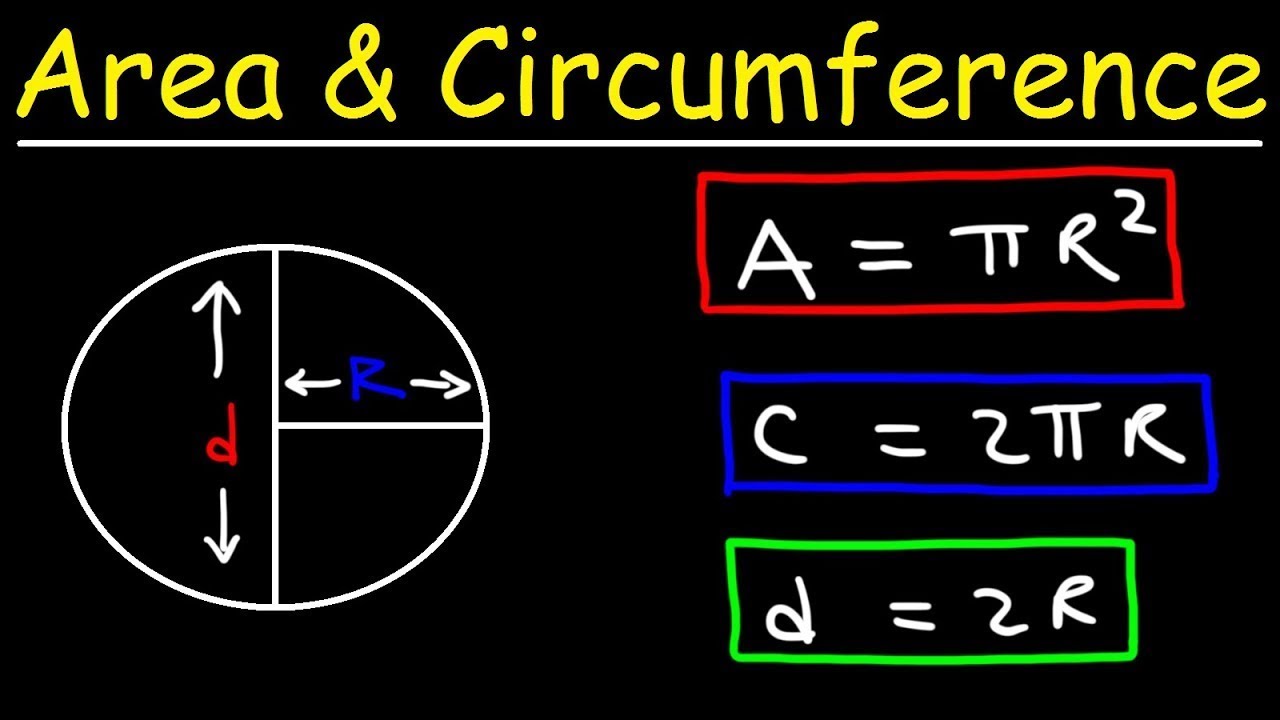
- 😀 The circumference is the perimeter of the circle and is calculated by multiplying the diameter by pi (π).
- 😀 The area of a circle is calculated using the formula: π times the square of the radius.
- 😀 Pi (π) is an irrational number, approximately 3.14159, and is commonly approximated as 3 for estimates.
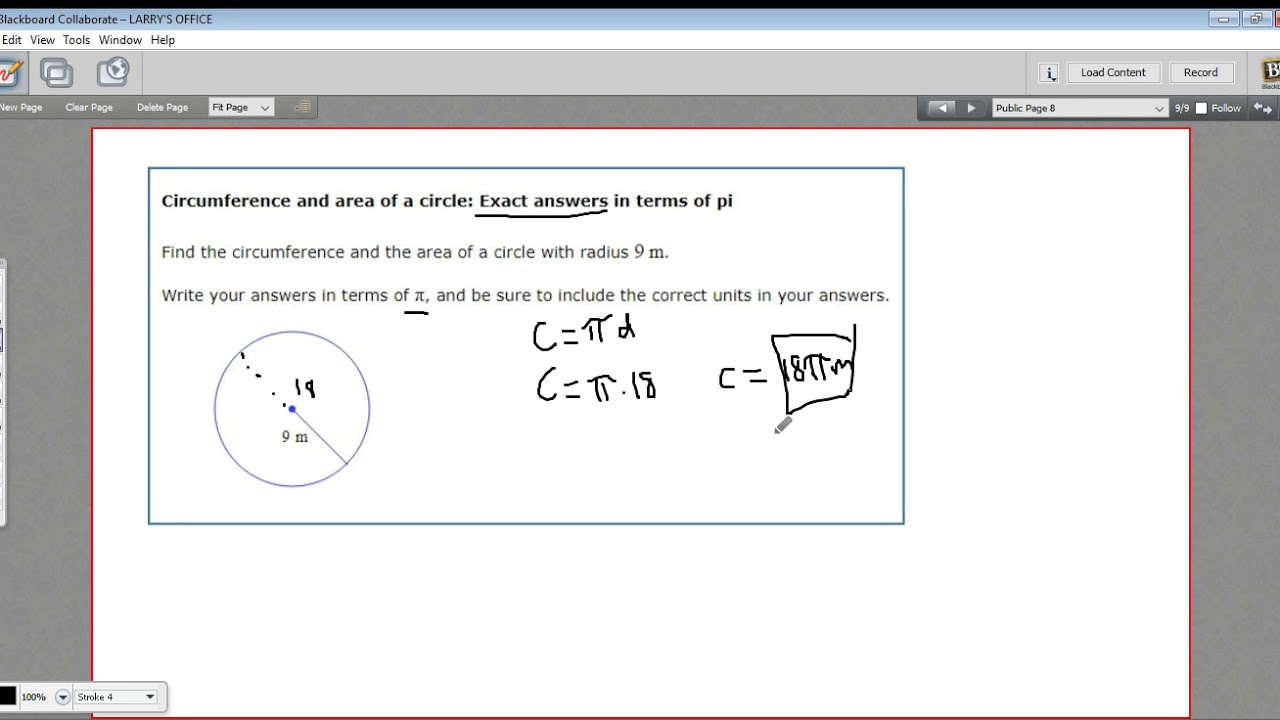
- 😀 To calculate the circumference, use the formula: Circumference = π × diameter.
- 😀 To calculate the area, use the formula: Area = π × radius².
- 😀 When estimating, you can round values such as the radius and pi to simplify calculations (e.g., rounding pi to 3).
- 😀 For precise calculations, it's best to use the pi button on calculators rather than approximating pi.
- 😀 The relationship between the radius and the diameter is that the diameter is always twice the length of the radius, and vice versa.
- 😀 In real-world problems, such as fencing a circular area, use the circumference formula to estimate costs by multiplying the circumference by a cost per meter.
Q & A
What is the radius of a circle?
-The radius of a circle is the distance from the center of the circle to the edge. It can be measured at any angle around the circle.
What is the diameter of a circle?
-The diameter is the distance across the circle, passing through the center. It is always twice the length of the radius.
How is the circumference of a circle calculated?
-The circumference of a circle is calculated using the formula: Circumference = π × Diameter.
How is the area of a circle calculated?
-The area of a circle is calculated using the formula: Area = π × (Radius²).
What is pi (π) and why is it used in circle calculations?
-Pi (π) is a mathematical constant approximately equal to 3.14. It represents the ratio of the circumference of any circle to its diameter and is used in formulas for circumference and area.
How do you calculate the circumference of a circle with a known diameter?
-To calculate the circumference, multiply the diameter by π. For example, if the diameter is 12 mm, the circumference is 12π mm.
How do you find the area of a circle given the radius?
-To find the area, square the radius and multiply it by π. For example, if the radius is 6 mm, the area is 36π mm².
What is the difference between estimating and calculating an exact value in circle problems?
-Estimating involves rounding values such as the radius or pi to simplify the calculation, which leads to an approximate result. Calculating the exact value uses the full, unrounded values for more precision.
If the radius is 9 cm, what is the diameter of the circle?
-The diameter is twice the radius, so if the radius is 9 cm, the diameter is 18 cm.
In the example with a circular paddock, how was the cost of fencing estimated?
-The radius of the paddock was 15 meters, giving a diameter of 30 meters. The circumference was estimated as 30 × 3 = 90 meters. The cost of fencing was then estimated by rounding the cost per meter to $10 and multiplying by 90 meters, giving an estimated cost of $900.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados
Circumference and area of a circle - exact answers in terms of pi

Cara Mencari Keliling dan Luas Lingkaran Jika Jari-jari dan Diameter Diketahui

Cara Menghitung Panjang Busur dan Luas Juring Lingkaran

Lingkaran dan Busur Lingkaran - Matematika SMA Kelas XI Kurikulum Merdeka
Circles - Area, Circumference, Radius & Diameter Explained!

How to Calculate Circumference of a Circle (Step by Step) | Circumference Formula
5.0 / 5 (0 votes)
