Enlargements - Corbettmaths

Summary

This video tutorial explains how to enlarge a right-angle triangle using a scale factor. The process involves identifying an object (the triangle), a point of enlargement (P), and the scale factor (2 in this case). The video demonstrates how each point of the triangle is doubled in distance from point P, resulting in a larger version of the original shape. The final enlarged triangle retains its properties, such as angles and shape, while the side lengths are doubled. The tutorial emphasizes the concept of enlargement and its practical application in geometry.

Takeaways

• 😀 The object to be enlarged is a shape, such as a right-angled triangle.
• 😀 To perform an enlargement, you need a point of enlargement (P).
• 😀 The scale factor determines how far the points move from the point of enlargement.
• 😀 In this example, the scale factor is 2, meaning all points will be twice as far from P.
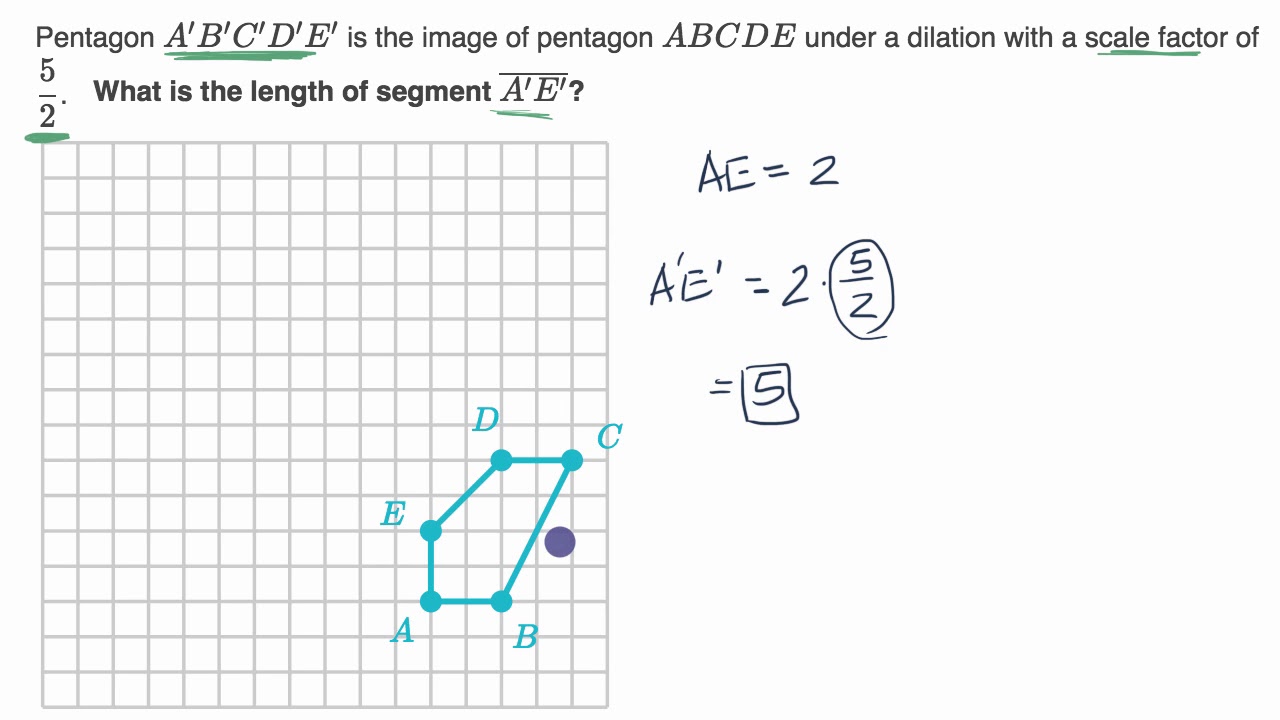
• 😀 The coordinates of point A are (4, -1). Doubling these gives A' at (8, -2).
• 😀 The coordinates of point B are (3, -3). Doubling these gives B' at (6, -6).
• 😀 The coordinates of point C are (4, -3). Doubling these gives C' at (8, -6).
• 😀 The enlarged shape retains the same form but is scaled by the factor of 2.
• 😀 The enlarged triangle is still a right-angled triangle, just with doubled dimensions.
• 😀 The length of each side of the triangle is doubled, but the shape remains proportional.
• 😀 The enlargement process involves both horizontal and vertical scaling of each point.

Q & A

What is the main focus of this lesson?

The main focus of this lesson is understanding how to enlarge a geometric shape, specifically a right-angled triangle, using a scale factor.

What is the first step in performing an enlargement?

The first step is to identify the object to be enlarged. In this case, the object is a right-angled triangle labeled ABC.

What is the second essential piece of information needed for enlargement?

The second essential piece of information is the point of enlargement, which is where the enlargement will be performed from. In this example, the point is labeled P.

What does the scale factor of 2 mean in this context?

A scale factor of 2 means that all points of the object will be moved twice as far away from the point of enlargement (P). This results in the object being enlarged to twice its original size.

How do you calculate the new position of point A after enlargement?

Point A originally has coordinates (4, -1). To enlarge it by a scale factor of 2, double both the horizontal and vertical distances from point P. This results in the new coordinates (8, -2) for point A'.

How do you calculate the new position of point B after enlargement?

Point B originally has coordinates (3, -3). To enlarge it by a scale factor of 2, double both the horizontal and vertical distances from point P. This results in the new coordinates (6, -6) for point B'.

How do you calculate the new position of point C after enlargement?

Point C originally has coordinates (4, -3). Doubling both the horizontal and vertical distances from point P gives the new coordinates (8, -6) for point C'.

What happens to the shape after performing the enlargement?

After performing the enlargement, the shape becomes larger, with all points moved according to the scale factor. The triangle A'B'C' retains its right angle and proportionality, but the side lengths are doubled.

How does the enlargement affect the base and height of the triangle?

The base and height of the triangle are both doubled. Originally, the base was 2 units, and the height was 2 units. After the enlargement, both the base and height become 4 units each.

How can you verify that the enlargement was done correctly?

You can verify the enlargement by checking that all points have moved the correct distance from the point of enlargement, and that the dimensions of the enlarged shape are exactly twice the size of the original. Additionally, the shape should remain proportional and maintain its angles.