🔵LA ELIPSE GEOMETRÍA ANALÍTICA [TRUCOS que necesitas saber ECUACIÓN GENERAL]🔵
Summary
TLDREn este video, el profesor explica de manera detallada y accesible el concepto de la elipse. Comienza con una definición sencilla utilizando dos puntos y un conjunto de puntos cuya distancia suma es constante. A través de un ejemplo práctico con hilo y clavos, muestra cómo construir una elipse. Luego, explica la relación entre los focos, los ejes mayor y menor, y cómo calcular las distancias utilizando fórmulas matemáticas. Además, aborda las elipses horizontales y verticales, proporcionando ejemplos y demostraciones claras para comprender cómo se aplican estas ecuaciones en situaciones reales.
Takeaways
- 😀 La elipse es el conjunto de puntos cuya suma de las distancias a dos puntos fijos (focos) es constante.
- 😀 Para construir una elipse, se puede usar un hilo amarrado a dos clavos colocados en los focos, y al trazar el hilo con el dedo se forma la figura.
- 😀 La ecuación general de una elipse horizontal es: x²/a² + y²/b² = 1, donde 'a' es el semi-eje mayor y 'b' es el semi-eje menor.
- 😀 Si la elipse es vertical, la ecuación cambia a: x²/b² + y²/a² = 1, donde 'a' es el semi-eje mayor y 'b' el semi-eje menor.
- 😀 Los focos de la elipse están situados a una distancia 'c' del centro, donde se cumple la relación a² = b² + c².
- 😀 El centro de la elipse es el punto medio entre los dos focos, y es donde se encuentran los ejes mayor y menor.
- 😀 Los puntos donde la elipse corta el eje mayor se llaman vértices, y donde corta el eje menor, se llaman co-vértices.
- 😀 La relación matemática entre los ejes de la elipse es que el eje mayor siempre tiene una longitud mayor que el eje menor.
- 😀 La longitud del lado recto de la elipse (la distancia perpendicular al eje mayor que pasa por los focos) se calcula como 2b²/a.
- 😀 Las elipses también pueden ser trasladadas o rotadas. En el caso de traslación, la ecuación se modifica para reflejar el nuevo centro de la elipse en (h, k).
Please replace the link and try again.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados

PROPORCIONALIDAD INVERSA. Explicación súper fácil!!!! 😊
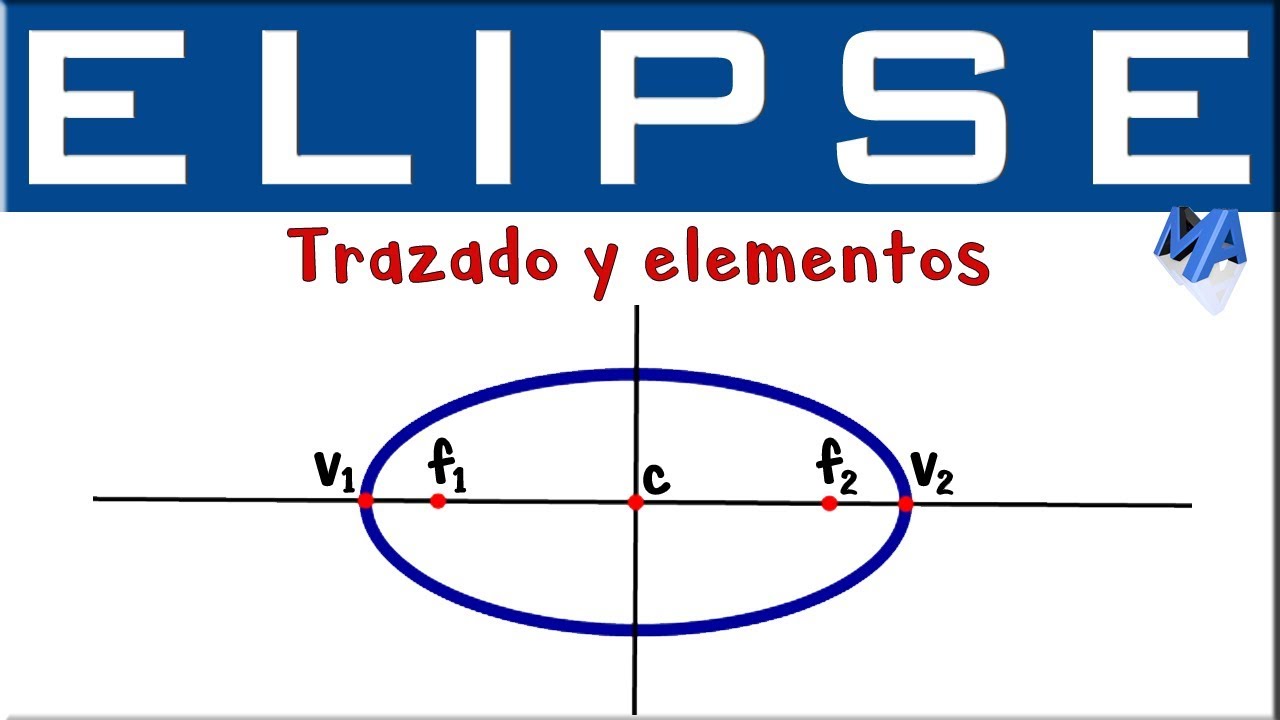
Elipse trazado y elementos | Introducción

✅ELIPSE con centro FUERA del ORIGEN [100% 𝙀𝙛𝙚𝙘𝙩𝙞𝙫𝙤 😎🫵💯] Geometría Analítica

Ecuación canónica de la Elipse | Centro (0,0)

¿Qué es MOOC?

Tipos de sistemas de ecuaciones lineales (análisis de las soluciones del sistema)

QUIMICA moles y número de AVOGADRO SECUNDARIA (4ºESO)
5.0 / 5 (0 votes)