Integral de una raíz | Ejemplo 2
Summary
TLDREn este video, el instructor explica cómo resolver integrales con raíces algebraicas, específicamente aquellas que contienen monomios. Se enseña a separar productos bajo raíces, reescribir raíces como potencias y aplicar reglas de integración para resolverlas. El proceso incluye simplificar expresiones, manejar constantes y realizar operaciones para obtener la solución final. Además, se invita a los estudiantes a practicar con un ejercicio al final, reforzando el aprendizaje. La explicación es clara y accesible, ideal para quienes buscan profundizar en el tema de integrales con raíces algebraicas.
Please replace the link and try again.
Q & A
¿Qué tipo de integrales se practican en este video?
-En este video se practican integrales de raíces, específicamente cuando dentro de la raíz hay un monomio algebraico, es decir, una expresión que involucra letras y números multiplicados.
¿Qué propiedad importante de las raíces se menciona en el video?
-Una propiedad importante de las raíces mencionada es que se puede separar una raíz de un producto. En este caso, se separa la raíz de 3x en dos raíces, raíz de 3 y raíz de x.
¿Por qué se puede separar la raíz de un producto?
-La raíz de un producto se puede separar utilizando la propiedad de radicación que establece que la raíz de un producto es igual al producto de las raíces individuales.
¿Qué se hace después de separar las raíces?
-Después de separar las raíces, se escribe la raíz como una potencia para poder integrar más fácilmente. Esto se hace siguiendo lo visto en el video anterior.
¿Cómo se convierte la raíz de x en una expresión más fácil de integrar?
-La raíz de x se convierte en una potencia al escribirla como x elevado a 1/2. Esto facilita la integración al tratarla como una expresión algebraica.
¿Qué pasa después de aplicar la integral?
-Después de aplicar la integral, el resultado es x elevado a 3/2, y luego se divide por 3/2. Esto se obtiene sumando 1 al exponente de 1/2 y simplificando la fracción.
¿Cómo se maneja la constante en la integración?
-Nunca se debe olvidar la constante de integración, que se agrega al final de la operación de integración.
¿Qué operación se realiza después de integrar la expresión?
-Después de la integración, se realizan operaciones de simplificación, como multiplicar las constantes y escribir la raíz cuadrada de x de nuevo como parte de la expresión final.
¿Qué se hace con la raíz cuadrada de x en el resultado final?
-La raíz cuadrada de x en el resultado final se mantiene dentro de la expresión, aunque se puede simplificar si es necesario. El video sugiere que, aunque se pueden hacer más simplificaciones, no siempre es necesario.
¿Cuál es el propósito del ejercicio al final del video?
-El propósito del ejercicio al final del video es que los estudiantes practiquen lo aprendido. Se les invita a resolver un ejercicio similar y luego comparar su respuesta con la correcta que se muestra en el video.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados

MONOMIO POR MONOMIO Super fácil - Para principiantes

Integral de una División - Fracción | Integrales por Sustitución - Cambio de variable | Ejemplo 2

¿Cómo derivar funciones con raíces?. [4 ejemplos]

Integrales definidas | Ejemplo 3
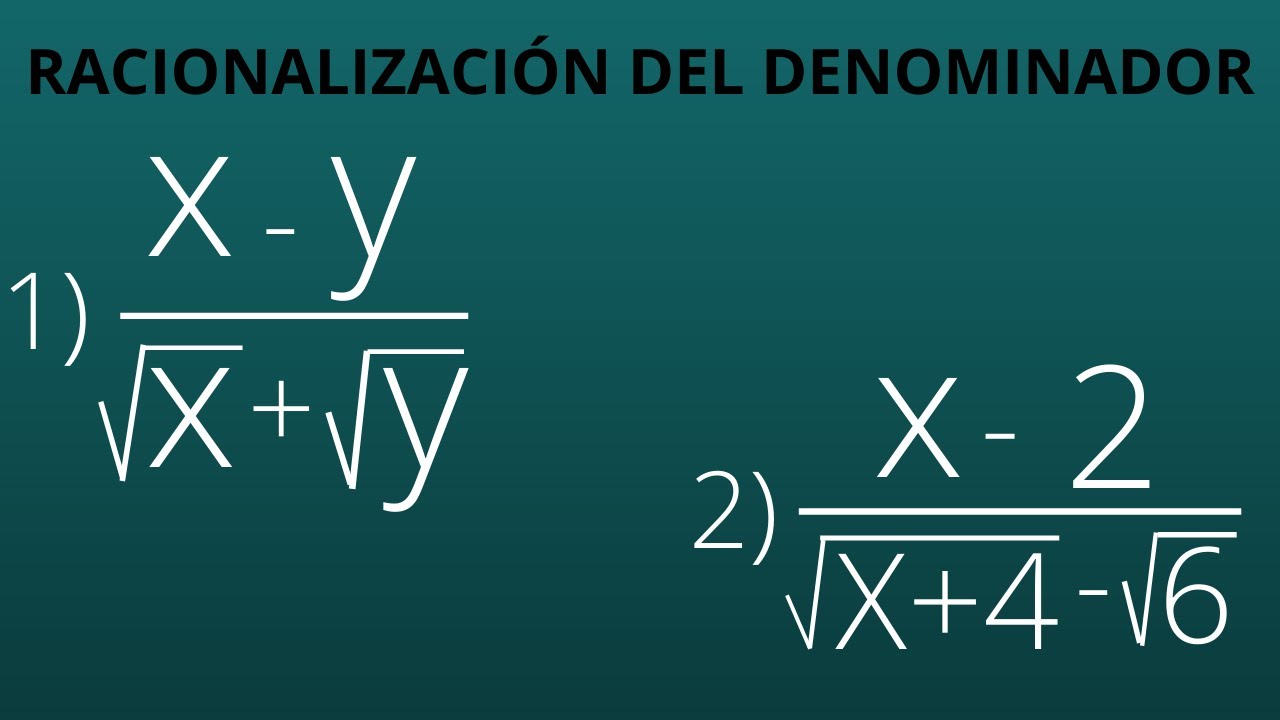
Racionalización del denominador (binomio) con expresiones algebraicas, explicado paso a paso.

01. Integral de una constante

Integración por sustitución | Ejemplo 11 | Seno
5.0 / 5 (0 votes)