Curso de Integrales. Capítulo 8: Método de Integración de Funciones Racionales I. Una prop. didact.
Summary
TLDREn este video, se explica cómo calcular la integral de una función racional, que es la división de dos polinomios. El presentador comienza por identificar si la integral es inmediata, mostrando un ejemplo donde la derivada del denominador aparece en el numerador. Si no es inmediata, se utiliza la división de polinomios para simplificar la expresión. Luego, se resuelve la integral resultante usando técnicas conocidas, como la integración logarítmica. Finalmente, se concluye con el cálculo de la integral para el caso específico, y se menciona que en el siguiente capítulo se abordarán casos con grados de polinomios diferentes.
Takeaways
- 😀 La integral de una función racional es la división de dos polinomios: un numerador y un denominador.
- 😀 A veces, aunque sea una división de polinomios, no es necesario aplicar un método si la integral es inmediata.
- 😀 Para comprobar si una integral es inmediata, se debe verificar si el numerador es la derivada del denominador.
- 😀 Un ejemplo inmediato es la integral de (12x^2 + 5) / (4x^3 + 5x), que es igual a ln(4x^3 + 5x).
- 😀 Si la derivada del denominador coincide con el numerador, la integral es inmediata y se resuelve con el logaritmo natural del denominador.
- 😀 Si la derivada del denominador no coincide con el numerador, se aplica el método de división de polinomios.
- 😀 El método de división de polinomios se aplica cuando el grado del numerador es mayor o igual al grado del denominador.
- 😀 Al dividir polinomios, el cociente más el resto dividido por el denominador da lugar a una nueva integral más fácil de resolver.
- 😀 Ejemplo de división de polinomios: 2x + 5 / x + 2, cuyo cociente es 2 y el resto es 1 / (x + 2).
- 😀 La integral de una suma es la suma de las integrales, lo que permite separar la integral original en varias más simples.
- 😀 Cuando la integral es de tipo logaritmo natural, se usa el valor absoluto para asegurar que el logaritmo esté bien definido para valores negativos.
- 😀 En resumen, si el grado del numerador es mayor o igual que el denominador, se divide y luego se resuelven las integrales inmediatas resultantes.
Please replace the link and try again.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados

Integral por descomposición en fracciones simples, integrales racionales

Asíntotas verticales, horizontales y oblicuas de una función racional
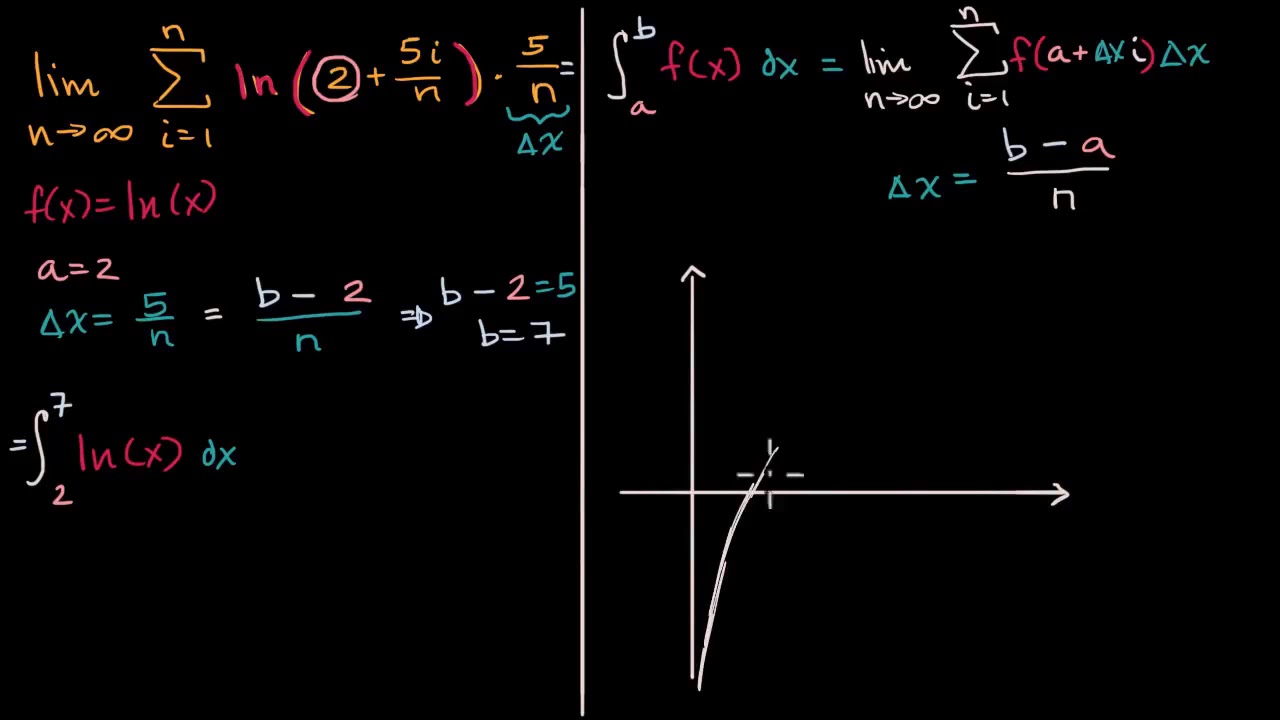
Escribir el límite de una suma de Riemann como una integral definida | Khan Academy en Español

Cálculo Integral - Tutorial de Área bajo la curva

Double Integral, definition as Double Riemann Sum, FULL EXPLANATION

Derivada de un producto o multiplicación de funciones. Cálculo diferencial
5.0 / 5 (0 votes)