Why a "least squares regression line" is called that...
Summary
TLDREste video explica el concepto de la línea de regresión de mínimos cuadrados, enfatizando su propósito y significado en el análisis estadístico. Se visualizan cinco puntos en un plano, sugiriendo una relación lineal. Se aborda la importancia de los residuos, que son las diferencias entre los puntos y la línea, y cómo minimizar la suma de los errores cuadrados para encontrar la mejor línea de ajuste. Además, se menciona el valor de correlación (R) como indicador de la calidad del ajuste. En resumen, la línea de regresión de mínimos cuadrados busca el ajuste que minimiza el error cuadrático entre los datos y la línea.
Takeaways
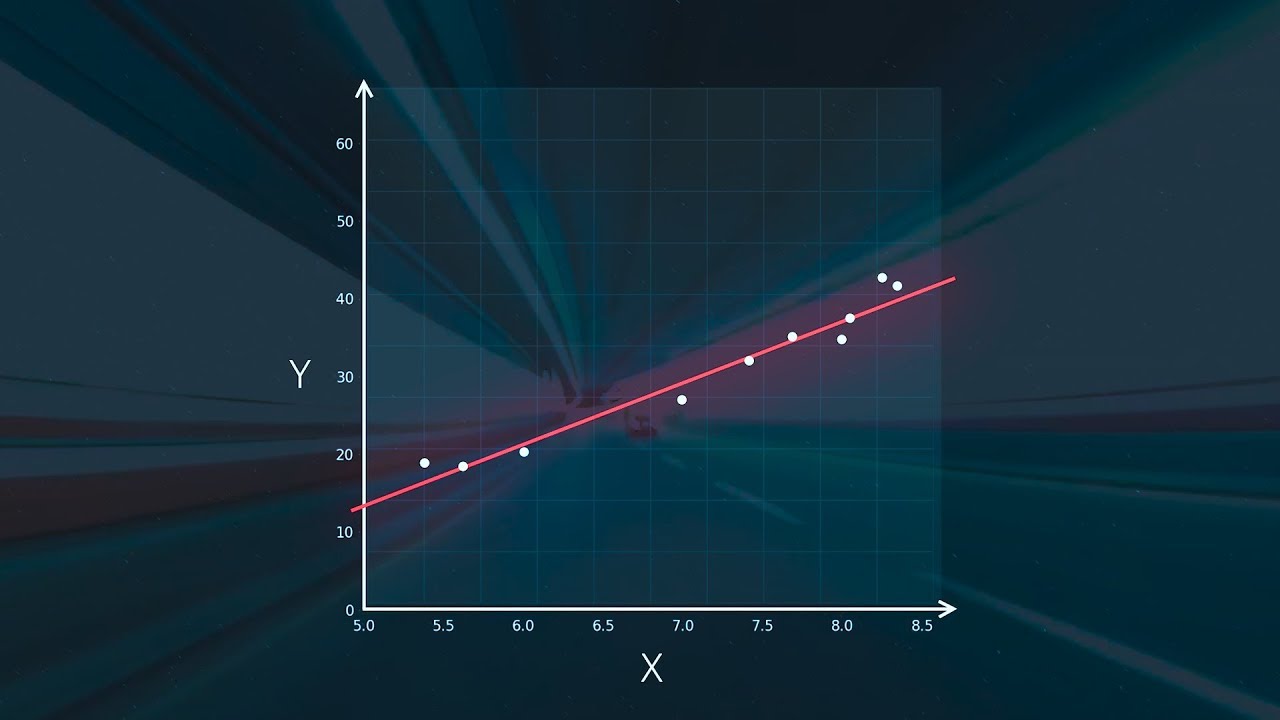
- 📊 La línea de regresión de mínimos cuadrados se utiliza para encontrar la mejor línea que describe un conjunto de puntos de datos.
- 📈 Al observar los puntos en el plano coordenado, es importante identificar si parecen seguir una tendencia lineal.
- 🔍 Se introducen los 'residuos' como medida de la diferencia entre los puntos de datos observados y los valores predichos por la línea.
- 🧮 La técnica de elevar al cuadrado los residuos ayuda a que todos los errores contribuyan positivamente al total de errores.
- ⚖️ El objetivo es minimizar la suma de los residuos cuadrados para encontrar la línea de mejor ajuste.
- 🔄 El presentador demuestra cómo al mover la línea más cerca de los puntos de datos, la suma de los residuos cuadrados disminuye.
- 💡 La línea de regresión de mínimos cuadrados es la que genera la menor suma de errores cuadrados, lo que indica un mejor ajuste.
- 📊 El valor de correlación y el valor R se utilizan para evaluar qué tan bien se ajusta el modelo lineal a los datos.
- ❓ Siempre es importante examinar los datos para decidir si una línea es la mejor forma de describir la relación entre ellos.
- 🔑 La comprensión del concepto de mínimos cuadrados es esencial para modelar datos de manera efectiva.
Q & A
¿Cuál es el propósito del video?
-El propósito del video es explicar por qué una línea de regresión de mínimos cuadrados se llama así.
¿Qué se presenta en el plano de coordenadas?
-Se presentan cinco puntos en el primer cuadrante del plano de coordenadas.
¿Qué deben hacer los estadísticos al analizar los datos?
-Los estadísticos deben observar si los datos parecen lineales antes de determinar la mejor línea de ajuste.
¿Qué son los residuos en el contexto de la regresión lineal?
-Los residuos son las diferencias entre los valores predichos por la línea de regresión y los valores reales de los datos.
¿Por qué la suma de los residuos debe ser cero en una línea de mejor ajuste ideal?
-En un mundo ideal, la suma de los residuos es cero porque los errores positivos y negativos se compensan entre sí.
¿Cómo los estadísticos abordan el problema de la suma de residuos cero?
-Los estadísticos abordan este problema al cuadrar las diferencias, lo que se utiliza en la medida de la desviación estándar.
¿Qué se entiende por 'mínimos cuadrados' en este contexto?
-El término 'mínimos cuadrados' se refiere a la técnica de minimizar la suma de los errores al cuadrar los residuos.
¿Cómo se visualiza el ajuste de la línea en el video?
-Se visualiza al mover la línea a través de los puntos de datos y observar cómo cambian las áreas de los cuadrados que representan los errores.
¿Qué es el valor de correlación mencionado en el video?
-El valor de correlación es una medida que indica cuán bien se ajusta la línea a los datos, pero no dice si una línea es la mejor opción para describir los datos.
¿Qué importancia tiene observar los datos antes de aplicar una regresión?
-Es importante observar los datos para decidir si una línea es un buen modelo para describir la relación entre las variables.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados

Regresión lineal simple 📊📈📉
Regresión Lineal y Mínimos Cuadrados Ordinarios | DotCSV

¿Que es un modelo de regresión lineal? explicado con manzanitas
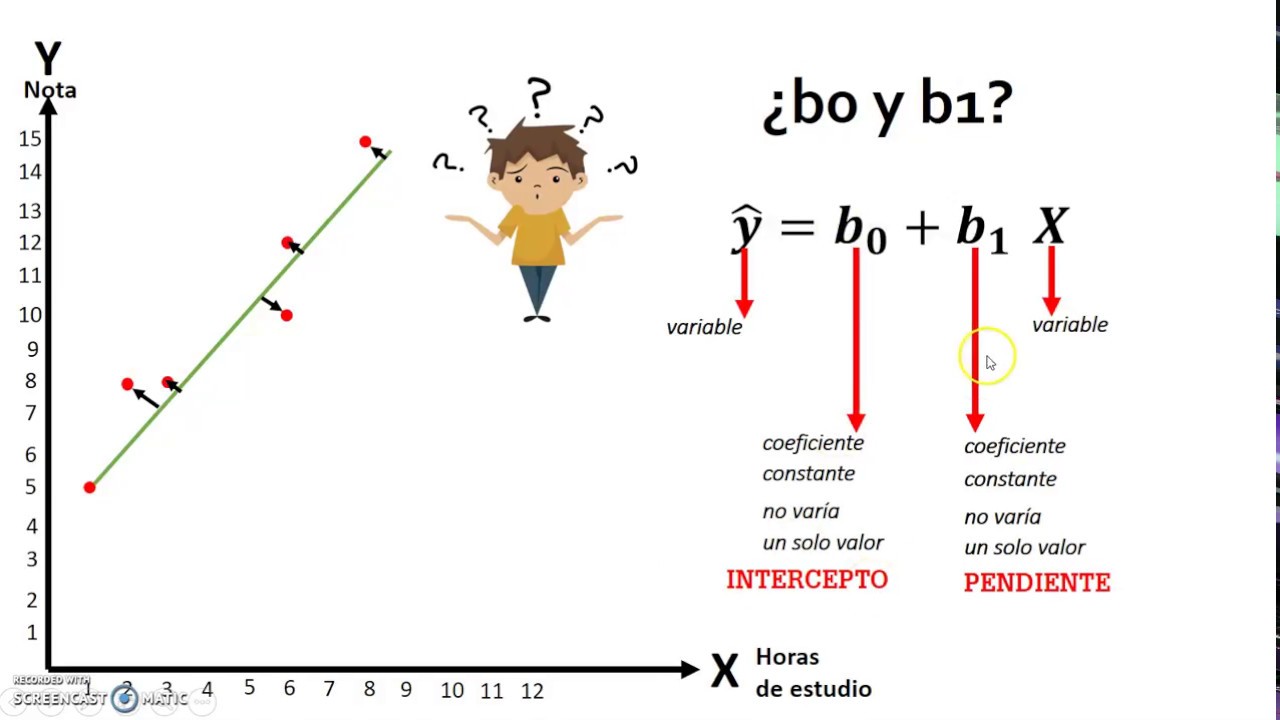
Regresión Lineal Simple (Parte 1)
EVIEWS TUTORIAL 1: ESTIMACIÓN DE UN MODELO CLÁSICO DE REGRESIÓN LINEAL (Indicadores y gráficos)

Cómo realizar el Análisis de Varianza ANOVA ✅ paso a paso en Excel

MÉTODO DE MÍNIMOS CUADRADOS
5.0 / 5 (0 votes)