What Linear Algebra Is — Topic 1 of Machine Learning Foundations
Summary
TLDRIn this video, John Crow introduces the fundamentals of linear algebra, focusing on its applications in machine learning. The tutorial covers data structures for algebra, tensor manipulation in Python, and matrix properties. It begins by explaining basic algebra and the differences between linear and nonlinear equations. The video also discusses solving systems of linear equations with practical examples and touches on modern uses of linear algebra in machine learning, including deep learning and regression models. The session ends with a brief history of algebra, leading into future discussions on tensors and matrix operations.
Takeaways
- 📚 This video is part of the Machine Learning Foundation series and focuses on an introduction to linear algebra, particularly tensor manipulation in Python.
- 🧮 Linear algebra deals with solving for unknowns within systems of linear equations, and the video provides examples using a simple sheriff and bank robber problem.
- 🟩 Key topics covered include data structures for algebra, tensor operations, and matrix properties, all aimed at practical applications in machine learning.
- 🔢 Algebra, generally, refers to arithmetic involving non-numerical entities, while linear algebra specifically excludes exponential or nonlinear transformations.
- 📈 A practical example is given, solving a system of linear equations to model how a sheriff catches a bank robber, illustrating basic linear algebra principles.
- 🏠 Linear algebra is essential for building models such as regression models, where multiple features like the distance to school or number of bedrooms help predict outcomes, such as house prices.
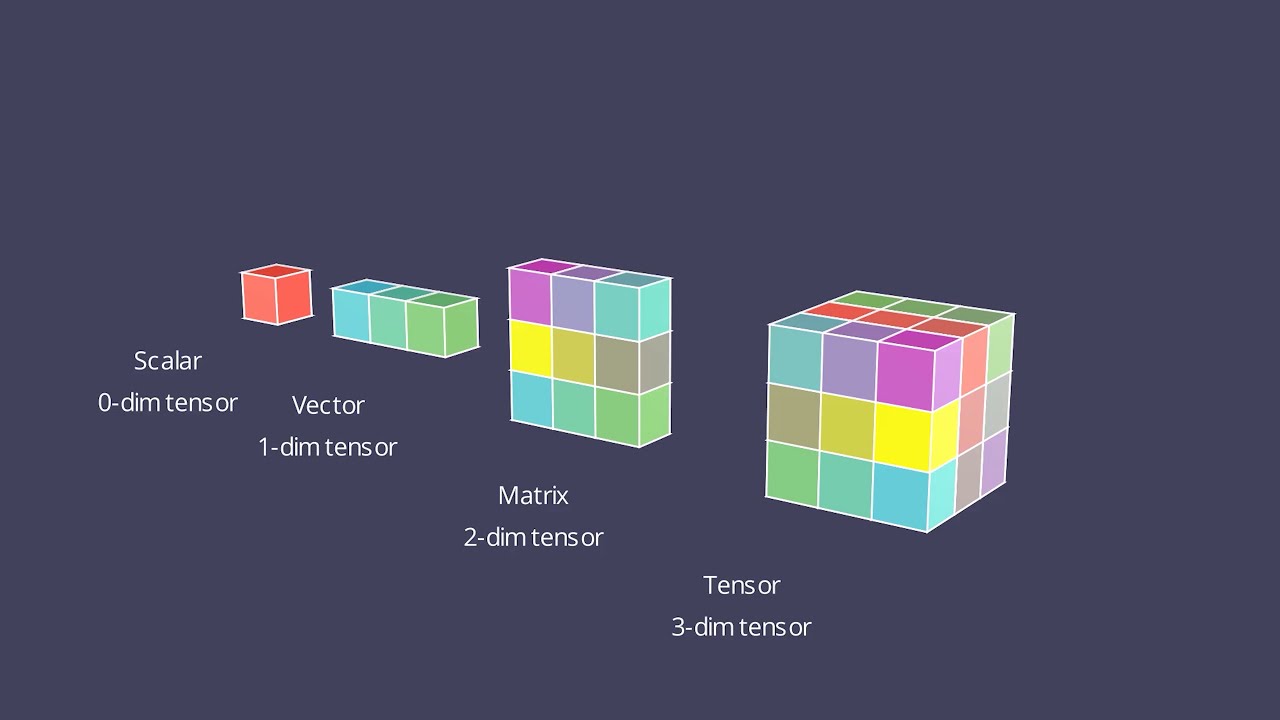
- 🤖 Linear algebra extends into deep learning, where tensors (multi-dimensional arrays) are used in machine learning models like convolutional neural networks.
- 🧠 TensorFlow and PyTorch are popular libraries for automatic differentiation and handling tensors in machine learning tasks.
- 🧑🏫 The history of algebra is briefly touched upon, crediting Persian mathematician Al-Khwarizmi for foundational contributions to the field and coining the term 'algorithm.'
- 🌐 Linear algebra has modern applications, including dimensionality reduction, web page ranking, recommendation systems, and natural language processing.
Q & A
What is the main focus of the 'Intro to Linear Algebra' video in this Machine Learning Foundation series?
-The video focuses on providing a primer on tensor manipulation in Python and covers the basics of linear algebra, including data structures, tensor operations, and matrix properties.
What are the three segments discussed in the 'Intro to Linear Algebra' course?
-The three segments are: 1) Data structures for algebra, 2) Common tensor operations, and 3) Matrix properties.
How does the video explain the basic concept of algebra?
-Algebra is defined as arithmetic that includes non-numerical entities, such as 'X'. The video demonstrates solving an equation like 2x + 5 = 25 to find that X equals 10.
What distinguishes linear algebra from general algebra?
-Linear algebra deals specifically with linear equations, which do not include terms with exponents, roots, or other non-linear transformations. It focuses on solving for unknowns within systems of linear equations.
What example is used to explain a system of linear equations?
-The example used is a scenario where a sheriff and a bank robber are driving at different speeds. The video explains how to find when and where the sheriff will catch the robber using a system of linear equations.
What are the three possible outcomes when solving a system of linear equations?
-The three outcomes are: 1) One solution, 2) No solution (if lines are parallel), and 3) Infinite solutions (if lines overlap completely).
How does linear algebra relate to machine learning?
-Linear algebra is fundamental in machine learning for tasks like solving regression models, optimizing parameters, and working with data structures such as tensors. It helps in modeling relationships and making predictions from data.
What role do tensors play in machine learning?
-Tensors, which are generalizations of matrices and vectors, are used to represent data in higher dimensions. They are key data structures in machine learning frameworks like TensorFlow and PyTorch, used to store inputs, weights, and outputs.
What historical mathematician is discussed in the video, and what is his contribution to algebra?
-The video discusses Abu Jafar Muhammad bin Musa Al-Khwarizmi, a Persian mathematician from the 9th century, who wrote a key text on algebra. His name also gave rise to the term 'algorithm.'
What are some modern applications of linear algebra mentioned in the video?
-Modern applications include solving systems of equations in machine learning models, dimensionality reduction with techniques like principal component analysis (PCA), and ranking web pages using eigenvectors.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados

LA01_Vectors

M4ML - Linear Algebra - 1.2 Motivations for linear algebra

Machine Learning Algorithms Overview - What all exist out there?

Machine Learning And Deep Learning - Fundamentals And Applications [Introduction Video]
V1. Data Types | Linear Algebra for Machine Learning #MathsforMachineLearning

M4ML - Linear Algebra - 1.1 Introduction: Solving data science challenges with mathematics
5.0 / 5 (0 votes)
