Factorización trinomio de la forma ax2+bx+c | Ejemplo 2
Summary
TLDREn este video se aborda la factorización de trinomios de la forma AX² + BX + C. El instructor explica paso a paso cómo organizar el trinomio, multiplicar y dividir por el coeficiente del término con mayor exponente, y luego aplicar la factorización utilizando paréntesis y simplificaciones. Además, se presentan dos formas válidas de llegar a la solución. Se ofrecen ejercicios prácticos y se invita a los espectadores a seguir aprendiendo en los próximos videos del curso de factorización. El video concluye animando a suscribirse, compartir y dar like.
Takeaways
- 😀 El curso trata sobre la factorización y enseña cómo factorizar trinomios de la forma AX^2 + BX + C.
- 🎓 Se recomienda revisar el primer video de la lista de reproducción para entender los conceptos básicos antes de continuar.
- 📝 Se debe asegurar que el trinomio esté ordenado antes de comenzar el proceso de factorización.
- 🔢 Se multiplica y se divide el trinomio por el número que está con la X al cuadrado, en este caso, el número 3.
- ➗ Se realiza la multiplicación y división en los términos del trinomio, recordando siempre incluir la multiplicación en los primeros dos términos y la división en el último.
- 👉 Se busca crear un trinomio de la forma X^2 + BX + C para facilitar el proceso de factorización.
- 🤔 Se deben encontrar dos números que, al multiplicarse, den el producto del término medio y, al restarse, den el término independiente del trinomio original.
- 📐 Se explica que hay dos posibles respuestas correctas para la factorización, dependiendo de cuál paréntesis se simplifica primero.
- 📚 Se aclaran los pasos para simplificar los términos dentro de los paréntesis, incluyendo la extracción de factores comunes y la reducción de fracciones.
- 📈 Se presentan ejercicios prácticos para que los estudiantes apliquen los conceptos aprendidos y se desafíen con trinomios de diferentes coeficientes.
- 🔗 Se invita a los estudiantes a explorar el curso completo de factorización en el canal del instructor y a interactuar con el contenido a través de suscripciones, comentarios y likes.
Q & A
¿Qué es la factorización por el trinomio de la forma AX^2 + BX + C?
-La factorización por el trinomio de la forma AX^2 + BX + C es un método para factorizar trinomios cuadráticos, donde se busca expresar el trinomio como la producto de dos binomios.
¿Cómo se determina si un trinomio se puede factorizar por este método?
-Se puede factorizar por este método si el trinomio está en el formato AX^2 + BX + C y se cumplen ciertas condiciones, como que el trinomio esté ordenado y que no haya la variable en el término independiente.
¿Qué es el primer paso al factorizar un trinomio por este método?
-El primer paso es asegurarse de que el trinomio esté ordenado, comenzando con el término de mayor exponente en la variable.
¿Cuál es la letra que se debe usar para el proceso de factorización?
-La letra que se debe usar es la que tiene el término con el exponente más alto, en este caso, la 'x'.
¿Cómo se multiplica y se divide el trinomio durante la factorización?
-Se multiplica y se divide el trinomio por el número que está con la variable de mayor exponente, en este caso, el número que está con la 'x' al cuadrado.
¿Qué se hace con el primer término al multiplicar por el número correspondiente?
-Se indica la multiplicación en el primer término, dejando el resultado entre paréntesis.
¿Qué sucede con el segundo término al multiplicar por el número correspondiente?
-También se indica la multiplicación en el segundo término, dejando el resultado entre paréntesis.
¿Cómo se determina el signo para los paréntesis en la factorización?
-El signo para los paréntesis se determina por la multiplicación de los signos correspondientes en los términos intermedios del trinomio.
¿Qué es la multiplicación de los dos y cómo se relaciona con la factorización?
-La multiplicación de los dos se refiere a la multiplicación de los dos números que, al ser multiplicados, deben dar el producto constante del término independiente, y al ser restados, deben dar el coeficiente del término medio.
¿Cómo se eligen los dos números para la factorización?
-Se eligen dos números que, al multiplicarse, den el producto constante del término independiente y, al restarse, den el coeficiente del término medio del trinomio.
¿Qué significa 'simplificar' en el contexto de la factorización?
-Simplificar en el contexto de la factorización significa reducir los coeficientes de los términos en los paréntesis hasta llegar a su menor expresión común.
¿Cuál es la importancia de recordar que la 'x' sin coeficiente es el número uno?
-Recordar que la 'x' sin coeficiente es el número uno es importante para no omitir el coeficiente implícito de 1 al factorizar, lo cual podría llevar a errores en la factorización.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados

Solución de límites por factorización | Ejemplo 10

Factorización Trinomio de la forma ax2+bx+c | Paso a paso

LOS 10 CASOS DE FACTORIZACION En 10 minutos Cursos online

7ºMÉTODO:TRINOMIO DE LA FORMA AX2+BX+C

Solución de límites por factorización | Ejemplo 4
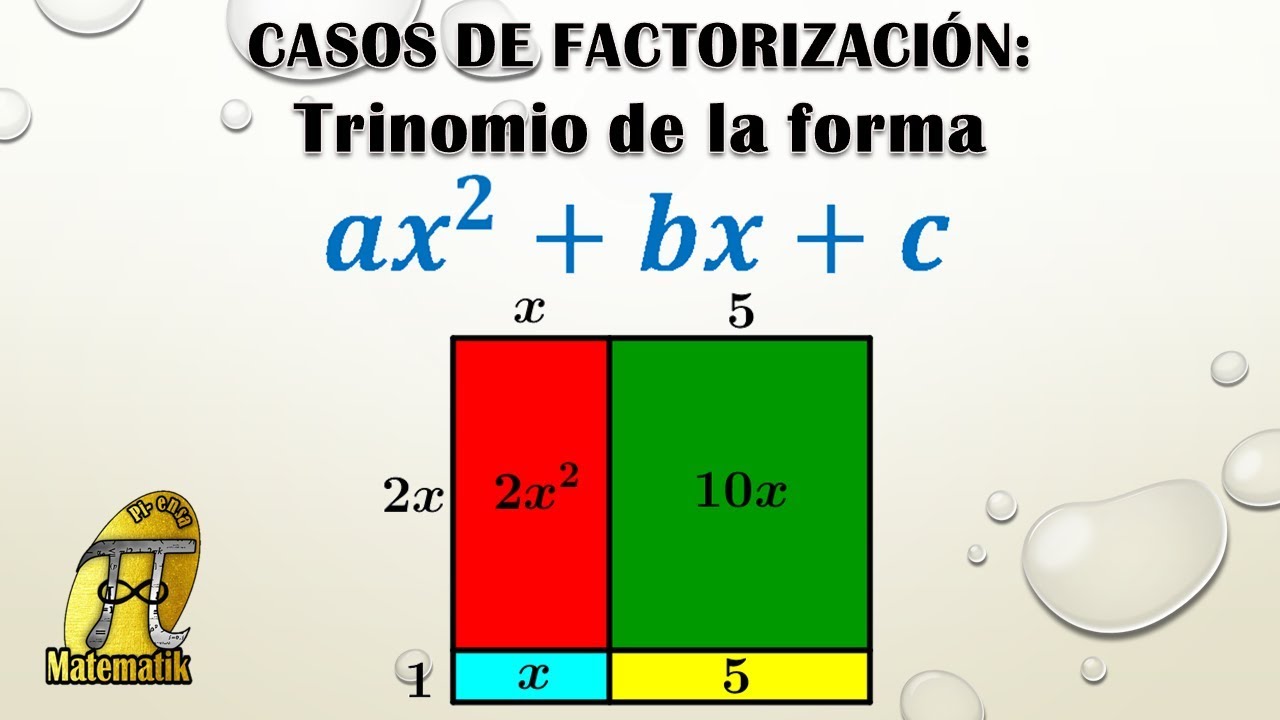
Trinomio de la forma ax^2+bx+c gráficamente | Casos de Factorización
5.0 / 5 (0 votes)