Método: rectángulos CIRCUNSCRITOS | Área bajo la curva | Cálculo Integral
Summary
TLDREn este video, se explica cómo calcular el área bajo la curva utilizando el método de los rectángulos circunscritos. El ejercicio se enfoca en encontrar el área limitada por la curva f(x) = x² + 1 y el eje x en el intervalo [0, 3], dividiéndolo en 6 subintervalos. El proceso incluye calcular el valor de cada subintervalo, graficar los puntos, y aplicar la fórmula del área. Finalmente, se suman los valores obtenidos y se multiplica por la altura de los subintervalos para encontrar el área total bajo la curva.
Takeaways
- 📐 El video explica cómo hallar el área bajo la curva utilizando el método de rectángulos circunscritos.
- 📊 El ejercicio se basa en la función f(x) = x^2 + 1, limitada por el eje x en el intervalo [0, 3].
- 🔢 Se utilizan 6 subintervalos para resolver el ejercicio, lo que implica dividir el intervalo en segmentos iguales.
- ➗ El valor de h, que es la longitud de cada subintervalo, se calcula como (b - a) / n, dando como resultado h = 0.5.
- 📈 La gráfica de la función puede trazarse manualmente o con software, como GeoGebra, y se usa para visualizar los rectángulos.
- 🔍 Los valores de la función se sustituyen en cada subintervalo, comenzando desde a = 0 y sumando múltiplos de h para obtener nuevos puntos.
- 🧮 Se calcula el valor de f(x) en puntos clave (0, 0.5, 1, 1.5, 2, 2.5, 3) para construir los rectángulos bajo la curva.
- 📏 Se omite el primer valor de a al calcular el área, ya que no representa la altura correcta del primer rectángulo.
- 🔗 La suma de las áreas de los rectángulos se multiplica por h, y el área total bajo la curva en el intervalo [0, 3] es 14.375 unidades cuadradas.
- 📝 El resultado final del área bajo la curva es el producto de 0.5 por la suma de las alturas de los rectángulos.
Q & A
¿Qué método se utiliza en el video para calcular el área bajo la curva?
-El método utilizado es el de los rectángulos circunscritos.
¿Cuál es la función que se usa en el ejercicio para calcular el área bajo la curva?
-La función utilizada es f(x) = x^2 + 1.
¿En qué intervalo se calcula el área bajo la curva en el ejercicio?
-El área se calcula en el intervalo [0, 3].
¿Cuántos subintervalos se consideran en este ejercicio?
-Se consideran 6 subintervalos.
¿Cómo se calcula el valor de cada subintervalo (h)?
-El valor de h se calcula como (b - a) / n, donde b es 3, a es 0 y n es 6, lo que da h = 0.5.
¿Qué valores se utilizan para calcular las alturas de los rectángulos?
-Se utilizan los valores a + h, a + 2h, a + 3h, etc., donde a es el valor inicial del intervalo.
¿Cuál es el valor de f(0.5) y cómo se obtiene?
-El valor de f(0.5) es 1.25, se obtiene sustituyendo 0.5 en la función f(x) = x^2 + 1.
¿Por qué no se considera el valor de f(0) en la fórmula para calcular el área?
-No se considera f(0) porque la altura del primer rectángulo sería incorrecta; la fórmula comienza con el valor f(a + h) para asegurar que se usen las alturas correctas.
¿Cuál es la suma de las alturas de los rectángulos?
-La suma de las alturas de los rectángulos es 28.75.
¿Cuál es el área bajo la curva obtenida en este ejercicio?
-El área bajo la curva es 14.375 unidades cuadradas.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados

Área bajo la curva por Extremos Derechos
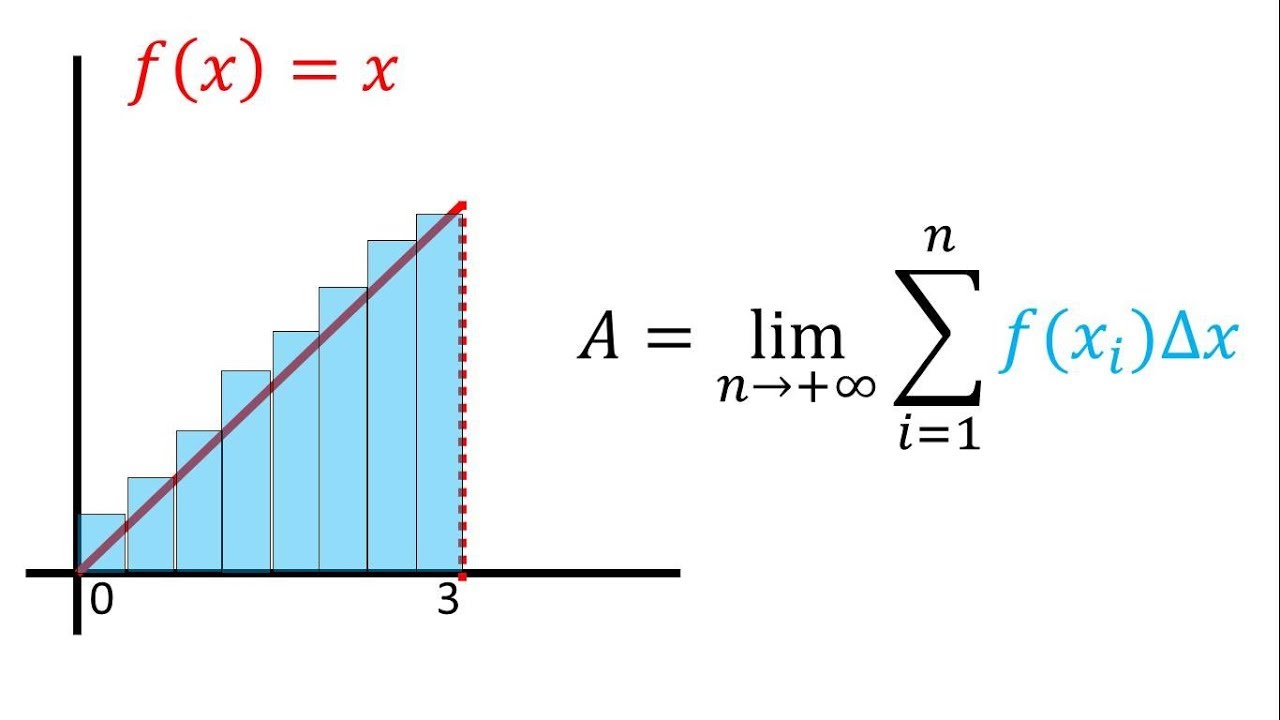
Área de una región plana utilizando sumatorias

Área bajo la curva por extremos izquierdos

Área bajo la curva (Cálculo integral) Método de rectángulos. EJEMPLO 2

Cálculo Integral 01:Área bajo una curva. Area under a curve
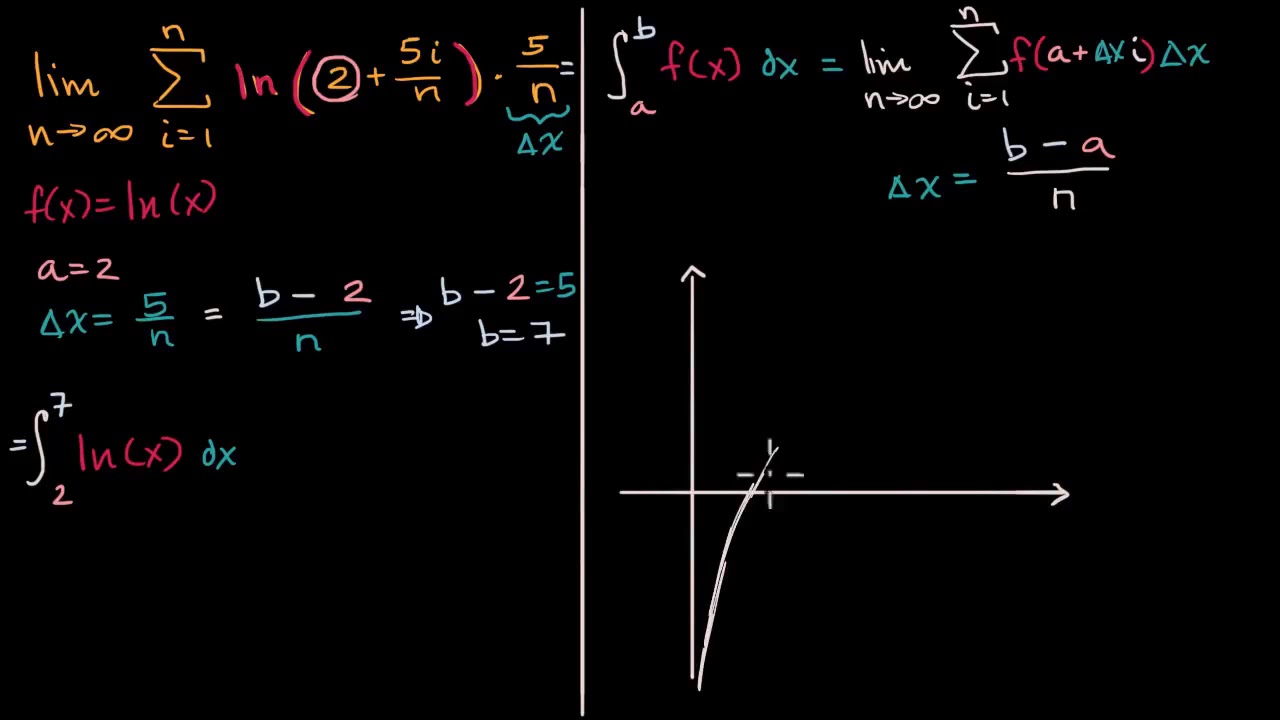
Escribir el límite de una suma de Riemann como una integral definida | Khan Academy en Español
5.0 / 5 (0 votes)