ÁREA DEL CÍRCULO A PARTIR DE POLÍGONOS REGULARES
Summary
TLDREl guion explora el cálculo del perímetro diario de polígonos regulares y el círculo. Se describe cómo el perímetro de un polígono regular inscrito en un círculo se acerca a la longitud de la circunferencia a medida que aumenta el número de lados. Se ilustra con triángulos equiláteros, hexágonos y polígonos con 24 lados, mostrando cómo el apotema y el radio tienden a coincidir. Finalmente, se explica que el área de un círculo se calcula como el área de un polígono regular con un número infinito de lados, resultando en la fórmula conocida de πr².
Takeaways
- 🔢 El perímetro diario de polígonos regulares y del círculo se calcula a partir de diferentes datos.
- 📐 Un polígono regular inscrito en un círculo significa que está encerrado dentro de él.
- 📏 Un triángulo equilátero inscrito en un círculo tiene su circunferencia dividida en tres arcos iguales.
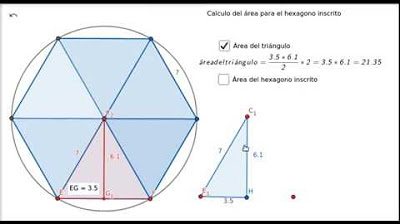
- 🔼 En un hexágono regular, la circunferencia está dividida en seis arcos iguales, proporcionando seis lados iguales.
- 📐 En un cuadrado inscrito, la circunferencia se divide en cuatro arcos iguales, y cada lado del cuadrado es perpendicular al radio.
- 🔄 Un polígono de 24 lados inscrito en una circunferencia es un polígono regular con 24 arcos iguales.
- 🔄 A medida que aumenta el número de lados de un polígono inscrito, su perímetro se aproxima a la longitud de la circunferencia.
- 📐 El radio y el apotema tienden a ser iguales en polígonos regulares inscritos en una circunferencia.
- 🔢 El perímetro de una circunferencia se calcula como π multiplicado por el diámetro, que es dos veces el radio.
- 📐 La fórmula para el área de un círculo se simplifica a π multiplicado por el radio al cuadrado, ya que el perímetro y el apotema se igualan al radio.
Q & A
¿Qué es un polígono regular inscrito en un círculo?
-Un polígono regular inscrito en un círculo es un polígono con todos sus vértices tocando el círculo, y todos sus lados y ángulos internos son iguales.
¿Cómo se relaciona el perímetro de un polígono regular con la circunferencia del círculo en el que está inscrito?
-El perímetro de un polígono regular inscrito en un círculo se aproxima a la longitud de la circunferencia del círculo a medida que el número de lados del polígono aumenta.
¿Qué es el apotema de un polígono regular inscrito?
-El apotema de un polígono regular inscrito es la distancia perpendicular desde el centro del círculo hasta el medio de uno de sus lados.
¿Cómo se calcula el área de un círculo a partir de la fórmula del área de un polígono regular?
-El área de un círculo se puede calcular sustituyendo el perímetro del círculo (2πr) y el apotema (r) en la fórmula del área de un polígono regular, que es (perímetro x apotema) / 2, resultando en πr^2.
¿Cuál es la relación entre el radio y el apotema en un polígono regular inscrito en un círculo?
-En un polígono regular inscrito en un círculo, el radio y el apotema tienden a ser iguales cuando el número de lados del polígono es grande, lo que se acerca a la definición de un círculo, que es considerado un polígono con un número infinito de lados.
¿Qué significa 'inscrito' en el contexto de polígonos y círculos?
-En el contexto de polígonos y círculos, 'inscrito' significa que todos los vértices de un polígono están tocando el círculo, formando una figura encerrada dentro del círculo.
¿Cómo se divide la circunferencia en arcos iguales por los vértices de un polígono regular inscrito?
-La circunferencia se divide en arcos iguales, donde el número de arcos es igual al número de lados del polígono regular inscrito.
¿Cuál es la fórmula para el perímetro de un polígono regular inscrito en un círculo si el número de lados es grande?
-Cuando el número de lados de un polígono regular inscrito en un círculo es grande, el perímetro se aproxima a la longitud de la circunferencia del círculo, que es 2πr, donde r es el radio del círculo.
¿Cómo se calcula el área de un polígono regular inscrito en un círculo si se conoce el radio del círculo?
-Si se conoce el radio del círculo, el área de un polígono regular inscrito se calcula sustituyendo el perímetro (2πr) y el apotema (r) en la fórmula del área del polígono regular, resultando en πr^2.
¿Qué observación se puede hacer sobre el tamaño del apotema en relación con el número de lados del polígono regular inscrito?
-A medida que aumenta el número de lados de un polígono regular inscrito en un círculo, el apotema tiende a ser más pequeño en comparación con el radio del círculo.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados

Áreas y perímetros de polígonos regulares | Explicado desde cero

Área de polígono inscrito en circunferencia- formula general

POLIGONOS REGULARES Super facil - Para principiantes

¿QUIÉN DESCUBRIÓ EL NUMERO π? - EL INICIO DE LA HISTORIA
Método de exhaución

PERIMETRO DE FIGURAS IRREGULARES Super facil - Para principiantes (POLIGONOS IRREGULARES)
5.0 / 5 (0 votes)